堆

堆(Heap)是一类特殊的数据结构，是最高效的优先级队列。

堆通常是一个可以被看做一棵树的数组对象(即用数组实现的树).

堆总是一棵完全二叉树。

从堆的根节点到任意叶节点画路径，总能得到从小到大（最小堆）的顺序或者从大到小（最大堆）的顺序。

由于堆是一颗完全二叉树，对于一个索引为 k 的节点，那么其左右儿子的索引则分别为 2k+1 和 2k+2（若存在）。

最大堆

最小堆

不满足完全二叉树，所以不是堆（值为19的节点缺失右儿子）

不是堆，堆一定满足从根节点画任意路径到一节点，其节点值总满足从大到小或者从小到大的顺序。

堆的操作

以下，我们就以最大堆为例，阐述堆的插入、删除、调整。

插入

因为堆中元素需要满足有序性，我们插入的值不一定就是这条路径中最小的，那么我们需要为元素找到合适的位置。 根据前文提到的堆的性质，我们可以确定当前节点的父节点所在位置是 i/2（对于 JavaScript 语言来说，需要向下取整）

假设我们现在要在这个堆中插入 98。

整个过程如下图所示：

首先扩展堆的容量 沿着父节点一直比较，直到找到合适的位置，这一过程中 i 一直不断的往上提，因为每次我们每次都是 i/2，这是一个类似二分查找的操作。 最终找到了合适的位置 完成插入 对于了解过排序算法的同学，对于这个过程是否感觉有些似曾相识？没错，这个过程就是直接插入排序。

调整和删除

为什么我们会把调整和删除一起讨论呢，主要是为了避免编写重复的代码。

假设，我们删除堆的一个元素，那么我们把数组下标为 0 的元素提出来，因为这个元素空出来了，相当于我们要把后面的元素往前挪动。但是 这儿可不能像数组那节说的那样挪动，否则会丢失顺序性。我们只能把最后一个元素交换到下标 0 的这个位置上来。然后重新调整堆。

好了，首先，我们先把看看当前节点(假设当前节点所在位置为 i)有没有左儿子(有的话，即2*i<length)，如果有，那我们看看当前节点是否有右儿子(有的话，即2*i+1<length)，若有的话，我们从两个儿子中取一个比较大的节点跟当前节点的值比较，如果大的儿子节点值大于 i 节点，那么把儿子节点较大的那个值拷贝到位置 i 上。并且把这个值放到大的儿子节点的那个位置上，然后 i 指向儿子节点较大者的那个索引；如果父节点比儿子节点的值还大，说明本来就保持了这个有序性，则可以不用变动。

因为我们刚才的操作其实是把影响下沉给了儿子节点，儿子节点现在不满足路径的顺序性质了，那么我们重复刚才的操作，直到调整到叶节点为止。

这一系列的过程，大概如下图所示：

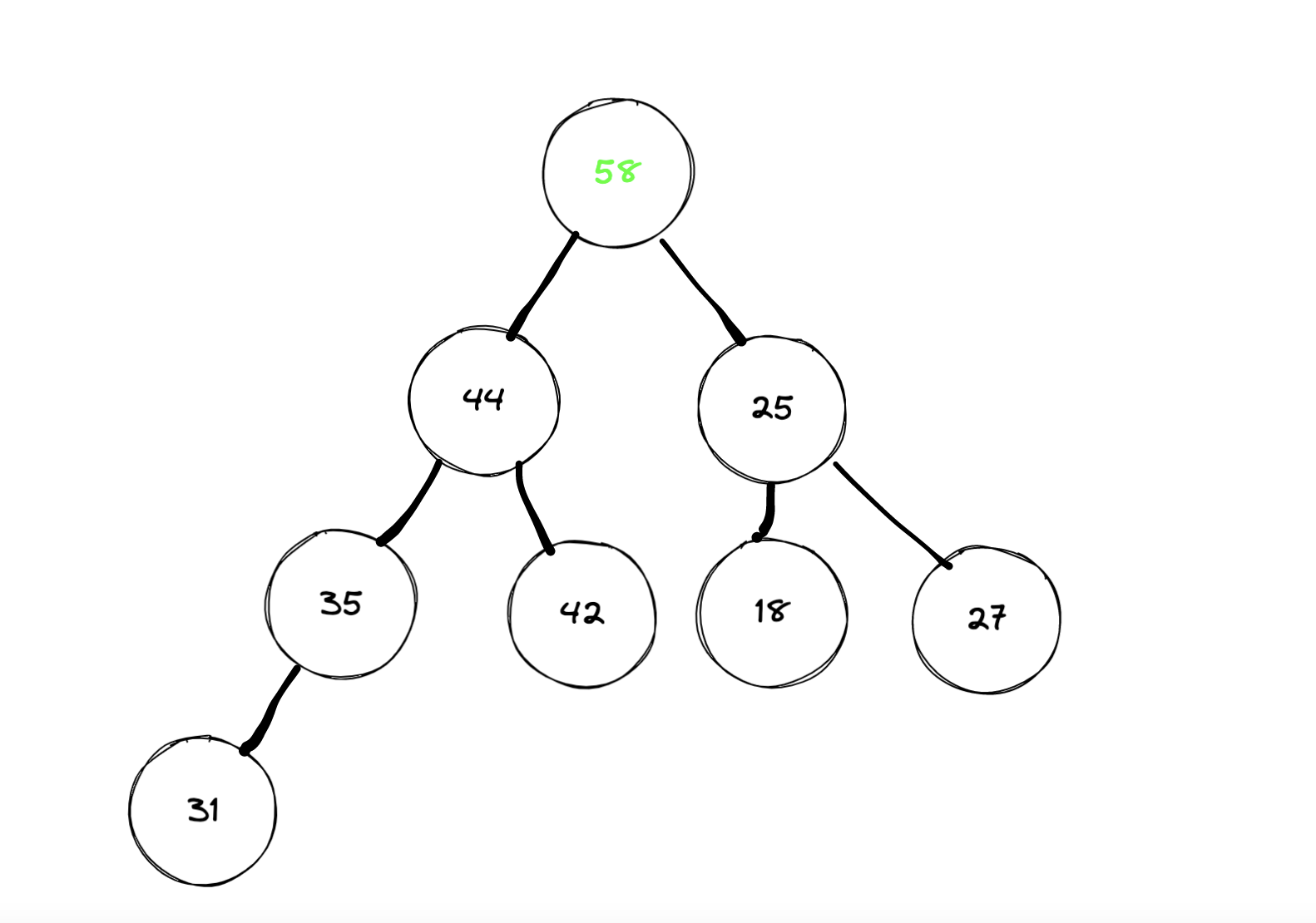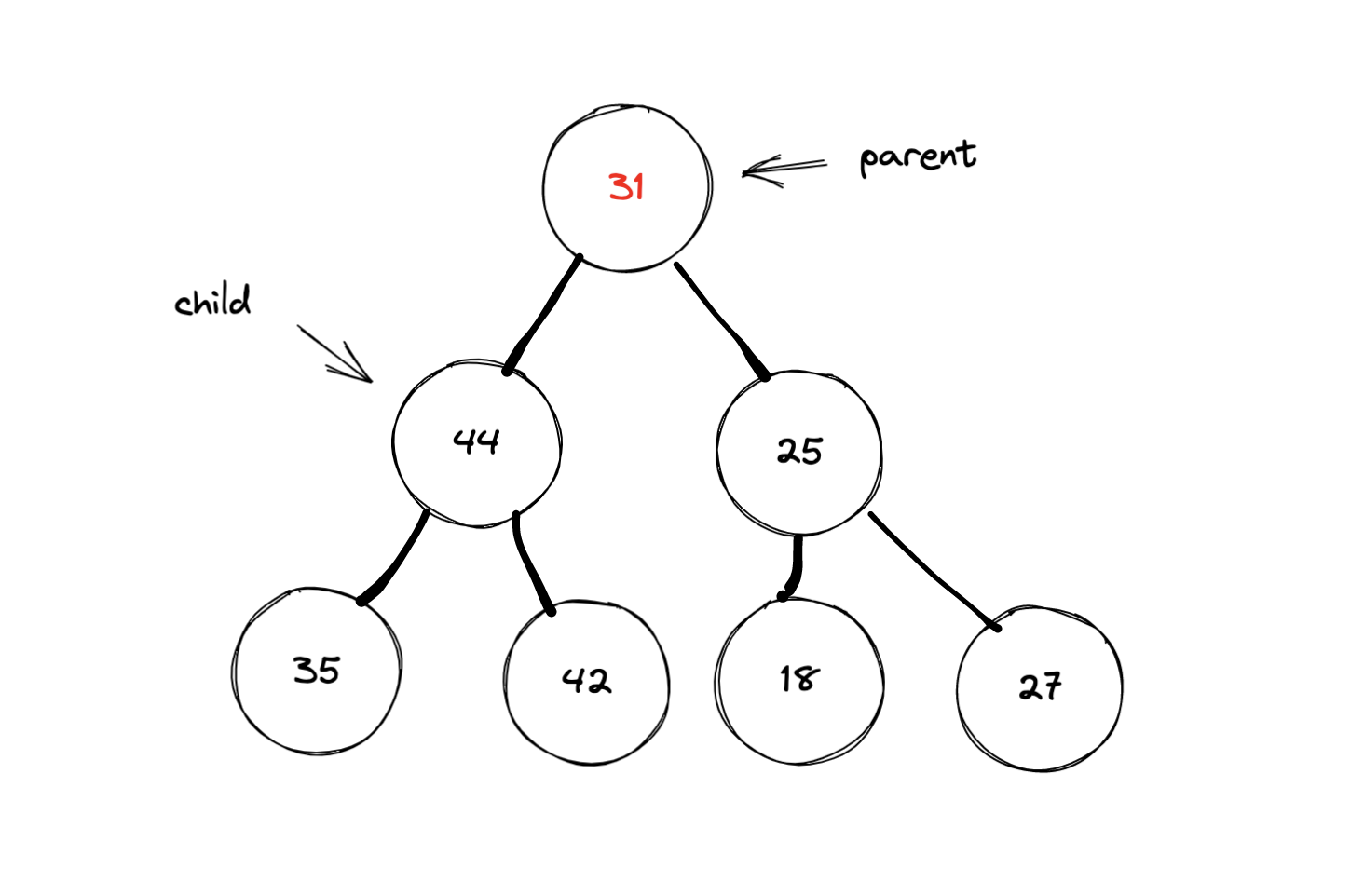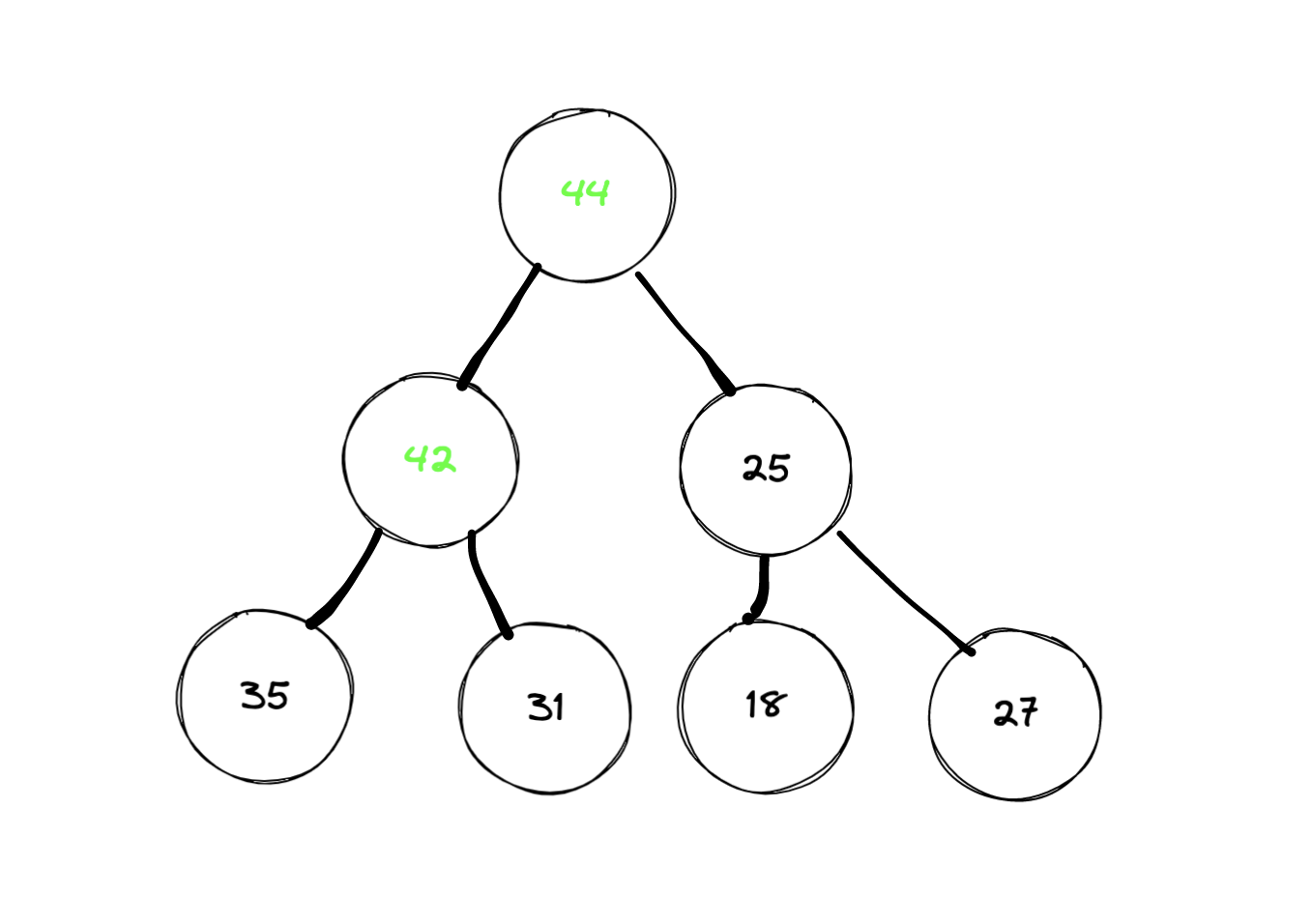
首先准备删除 然后将节点值拷贝到根节点，然后把已经拷贝好值的节点拿掉； 因为子节点比跟节点的值大，所以，将子节点向上提，parent 指针指向被影响的儿子节点的位置 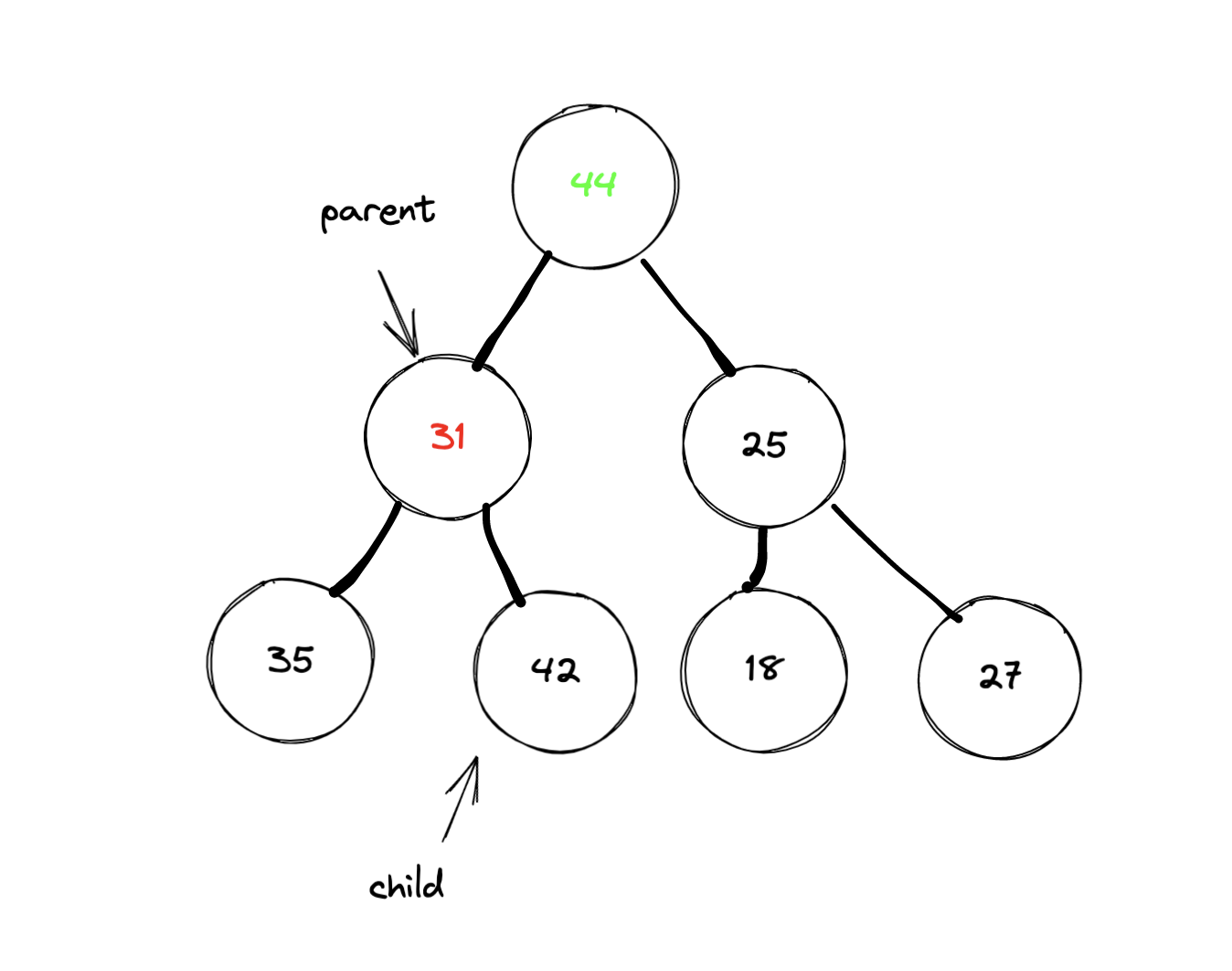重复这个过程，直到把这个影响传递到叶节点，则完成调整。

构建

之前我们已经理解了怎么样以根节点 p 把一个被破坏了的堆还原。如何把一个数组调整成堆呢，我们首先知道一个数组的最后一个节点的，那么根据这个节点，可以推算出它的父节点。我们首先把它们俩调整成堆。接着，我们把这个父节点的左边兄弟节点调整成堆，然后再把父节点的左边的兄弟左边的兄弟节点调整成堆，重复这个操作，直到调整到数组的第 1 个节点，就可以使得我们整个数组调整为堆。这个过程是个线性的时间复杂度，具体推导，读者可自行查阅资料，本节不做具体分析。

上述过程的算法实现如下：

/*
 * 最大堆
 */
class Heap {
  /**
   * 定义一个存储数据的内存空间
   */
  _data = [];

  get size() {
    return this._data.length;
  }

  constructor(...nums) {
    // 初始化数组元素
    nums.forEach((v) => {
      this._data.push(v);
    });
    this.buildHeap();
  }

  /**
   * 获取堆顶的元素
   */
  getTop() {
    return this._data[0];
  }

  /**
   * 按断堆是否是空
   */
  isEmpty() {
    return this._data.length === 0;
  }

  /**
   * 向堆中插入一个合法值
   * @param {number} val
   */
  insert(val) {
    // 如果当前数组没有元素，直接插入即可
    if (this._data.length === 0) {
      this._data[0] = val;
    } else {
      // 让i指向当前新位置，因为没有哨兵的关系，最后一个元素是length - 1，所以新位置就是length
      let i = this.size;
      while (val > this._data[Math.floor(i / 2)] && i > 0) {
        this._data[i] = this._data[Math.floor(i / 2)];
        i = Math.floor(i / 2);
      }
      // 在合适的位置插入新的值
      this._data[i] = val;
    }
  }

  /**
   * 获取堆中的最大元素
   * @returns
   */
  deleteMax() {
    if (this.isEmpty()) {
      console.warn("can not delete max from empty heap");
      return;
    }
    // 取出堆顶的元素
    let minVal = this._data[0];
    // 把堆最后的元素交换到堆顶去
    let temp = this._data[this.size - 1];
    this._data[0] = temp;
    // JavaScript语言需要进行这一步，让数组的规模缩小，释放空间
    this._data.length--;
    // 将数组调整成堆
    this.percDown(0);
    return minVal;
  }

  /**
   * 下滤：将堆中以堆data[p]为根的子堆调整为最小堆
   * @param {number} p 根节点索引
   */
  percDown(p) {
    // 如果当前堆元素小于1个，就不执行调整操作
    if (this.size <= 1) {
      return;
    }
    let parent, child;
    /* 取出根结点存放的值 */
    let temp = this._data[p];
    for (parent = p; parent * 2 < this.size; parent = child) {
      child = parent * 2;
      /* 如果右儿子存在 child指向左右子结点的较大者 */
      if (child + 1 < this.size && this._data[child + 1] > this._data[child]) {
        child++;
      }
      /* 找到了合适位置 */
      if (temp >= this._data[child]) {
        break;
      } else {
        /* 下滤X */
        this._data[parent] = this._data[child];
      }
    }
    this._data[parent] = temp;
  }

  /**
   * 构建最大堆
   */
  buildHeap() {
    /* 调整data中的元素，使满足最小堆的有序性  */
    /* 这里所有size个元素已经存在data[]中 */
    /* 从最后一个结点的父节点开始，到根结点1 */
    for (let i = Math.floor((this.size - 1) / 2); i >= 0; i--) {
      this.percDown(i);
    }
  }
}

带哨兵的堆的操作

哨兵

在查找时，通过设置哨兵能够省去对一些边界条件的判断，减少比较次数，有利于提高程序的效率和健壮性。

堆带哨兵和不带哨兵的区别

• 不能在堆中插入大于哨兵的元素，否则哨兵失去意义还会给程序带来问题。
• 对于索引为 k 的节点，左右儿子的下标索引也有变化，分别为 2k 和 2k+1(若存在)
• 在堆的插入操作时，不需要判断 i 的下标大于 0，因为哨兵自带判断依据，也不需要判断堆内元素为空的情况。
• 在删除堆的最大值之后，需要将最后一个节点的元素拷贝到下标为 1 的位置，而不是 0
• 在下滤时，外层循环终止条件发生变化，需要取到length，原为[0，length-1]。
• 在构建堆时，是从length/2开始到 1 结束

/*
 * 最大堆
 */
class Heap {
  /**
   * 定义哨兵的最大值，所有插入堆的元素都必须比这个值小
   */
  #MAX_VAL = 1000;

  /**
   * 定义一个存储数据的内存空间
   */
  #data = [];

  /**
   * 当前堆的元素个数
   */
  #size = 0;

  constructor(...nums) {
    // 设置哨兵
    this.#data[0] = this.#MAX_VAL;
    // 初始化数组元素
    nums.forEach((v, i) => {
      this.#data[i + 1] = v;
      this.#size++;
    });
    this.buildHeap();
  }

  isEmpty() {
    return this.#size === 0;
  }

  /**
   * 向堆中插入一个合法值
   * @param {number} val
   */
  insert(val) {
    if (this.MAX_VAL <= val) {
      throw `can not insert val bigger than ${this.#MAX_VAL}`;
    }
    // 堆的容量扩充1
    this.#size++;
    // 让i指向当前新位置
    let i = this.#size;
    // 因为有哨兵的关系，不需要添加约束条件 i > 0
    while (this.#data[Math.floor(i / 2)] < val) {
      this.#data[i] = this.#data[Math.floor(i / 2)];
      i = Math.floor(i / 2);
    }
    this.#data[i] = val;
  }

  deleteMax() {
    if (this.isEmpty()) {
      console.warn("can not delete max from empty heap");
      return;
    }
    // 取出堆顶的元素
    let maxVal = this.#data[1];
    // 取出堆最后一个元素 取出来之后则把堆的规模减小
    let temp = this.#data[this.#size--];
    this.#data[1] = temp;
    this.percDown(1);
    // JavaScript语言需要进行这一步，让数组的规模缩小，释放空间
    this.#data.length--;
    return maxVal;
  }

  /* 下滤：将堆中以堆data[p]为根的子堆调整为最大堆 */
  percDown(p) {
    let parent, child;
    let temp = this.#data[p]; /* 取出根结点存放的值 */
    // 虽然不带哨兵，但是因为外界传递的索引是预期的，所以还是只能按不带索引的计算方式计算
    for (parent = p; parent * 2 <= this.#size; parent = child) {
      child = parent * 2;
      if (child != this.#size && this.#data[child] < this.#data[child + 1]) {
        child++; /* child指向左右子结点的较大者 */
      }
      /* 找到了合适位置 */
      if (temp >= this.#data[child]) {
        break;
      } else {
        /* 下滤X */
        this.#data[parent] = this.#data[child];
      }
    }
    this.#data[parent] = temp;
  }

  /*----------- 建造最大堆 -----------*/
  buildHeap() {
    /* 调整data中的元素，使满足最大堆的有序性  */
    /* 这里所有size个元素已经存在data[]中 */
    /* 从最后一个结点的父节点开始，到根结点1 */
    for (let i = Math.floor(this.#size / 2); i > 0; i--) {
      this.percDown(i);
    }
  }
}

进阶

在上述堆的代码实现中，我们可以看到，想控制一个堆的性质（最大堆还是最小堆），仅仅改变一下判断依据就好了。

那么，上述的代码就可以进行抽象，我们将它封装成一个通用的堆，移植到成熟的代码库中去，这样就可以避免每次都复制粘贴代码了。

/*
 * 抽象堆
 */
class Heap {
  /**
   * 定义一个存储数据的内存空间
   */
  _data = [];

  /**
   * 比较函数
   */
  _compare = null;

  get size() {
    return this._data.length;
  }

  _selfCompare = (compareVal, currentVal) => {
    if (typeof this._compare !== "function") {
      throw `cannot compare without a compare function`;
    }
    return this._compare(compareVal, currentVal);
  };

  /**
   * 设置比较函数
   * @param {(compareVal, currentVal) => boolean} compareFunc
   */
  setCompare(compareFunc) {
    this._compare = compareFunc;
  }

  /**
   * 获取堆顶的元素
   */
  getTop() {
    return this._data[0];
  }

  /**
   * 按断堆是否是空
   */
  isEmpty() {
    return this._data.length === 0;
  }

  /**
   * 向堆中插入一个合法值
   * @param {number} val
   */
  insert(val) {
    // 如果当前数组没有元素，直接插入即可
    if (this._data.length === 0) {
      this._data[0] = val;
    } else {
      // 让i指向当前新位置，因为没有哨兵的关系，最后一个元素是length - 1，所以新位置就是length
      let i = this.size;
      while (this._selfCompare(val, this._data[Math.floor(i / 2)]) && i > 0) {
        this._data[i] = this._data[Math.floor(i / 2)];
        i = Math.floor(i / 2);
      }
      // 在合适的位置插入新的值
      this._data[i] = val;
    }
  }

  /**
   * 获取堆中的最值元素
   * @returns
   */
  deleteTop() {
    if (this.isEmpty()) {
      console.warn("can not delete max from empty heap");
      return;
    }
    // 取出堆顶的元素
    let minVal = this._data[0];
    let temp = this._data[this.size - 1];
    this._data[0] = temp;
    // JavaScript语言需要进行这一步，让数组的规模缩小，释放空间
    this._data.length--;
    // 如果当前堆里面还存在元素的话，将
    this.percDown(0);
    return minVal;
  }

  /**
   * 下滤：将堆中以堆data[p]为根的子堆调整为最小堆
   * @param {number} p 根节点索引
   */
  percDown(p) {
    // 如果当前堆元素小于1个，就不执行调整操作
    if (this.size <= 1) {
      return;
    }
    let parent, child;
    /* 取出根结点存放的值 */
    let temp = this._data[p];
    for (parent = p; parent * 2 < this.size; parent = child) {
      child = parent * 2;
      if (
        child + 1 < this.size &&
        this._selfCompare(this._data[child + 1], this._data[child])
      ) {
        child++; /* child指向左右子结点的较大者 最大堆 较小者 最小堆 */
      }
      /* 找到了合适位置 */
      // 注意这儿一定要取得等号 temp <= this.#data[child] 最小堆 temp >= this.#data[child] 最大堆
      if (this._selfCompare(temp, this._data[child])) {
        break;
      } else {
        /* 下滤X */
        this._data[parent] = this._data[child];
      }
    }
    this._data[parent] = temp;
  }

  /**
   * 构建最小堆
   */
  buildHeap() {
    /* 调整data中的元素，使满足最小堆的有序性  */
    /* 这里所有size个元素已经存在data[]中 */
    /* 从最后一个结点的父节点开始，到根结点1 */
    for (let i = Math.floor((this.size - 1) / 2); i >= 0; i--) {
      this.percDown(i);
    }
  }
}

class MinHeap extends Heap {
  constructor() {
    super();
    this.setCompare((compareVal, currentVal) => {
      return compareVal - currentVal <= 0;
    });
  }

  getMin() {
    return this.getTop();
  }

  deleteMin() {
    return this.deleteTop();
  }
}

class MaxHeap extends Heap {
  constructor() {
    super();
    this.setCompare((compareVal, currentVal) => {
      return compareVal - currentVal >= 0;
    });
  }

  getMax() {
    return this.getTop();
  }

  deleteMax() {
    return this.deleteTop();
  }
}

如果堆的元素是个对象，我们可以手动设置比较函数，也可以达到相应的效果

比如：

// 假设我们将这个抽象堆封装至代码库中了
import { Heap } from "awesome-frontend-code";
const maxHeap = new Heap();
// 现在需要根据学生的成绩建堆。
maxHeap.setCompare((compareStudent, currentStudent) => {
  return compareStudent.score - currentStudent.score >= 0;
});

应用场景

堆的应用场景比较模糊，但是我根据自己的实际体验和与朋友们的交流大致总结了 2 个场景：

• 想让序列保持有序，但是又不想直接使用排序算法。
• 动态的数据，无法每次数据改变都进行排序，但是最终却需要有序的序列。