洗牌算法

洗牌算法，是D.E.Knuth教授改进之后的算法，是不是觉得这个名字有点儿熟悉？对，你记性真好呢，KMP算法的K就是来源于唐纳德教授的名字。

这个算法的思路理解起来也比较简单，接下来我们就描述一下这个算法的执行过程，并分析它是如何保证数据能够被等概率打乱的。

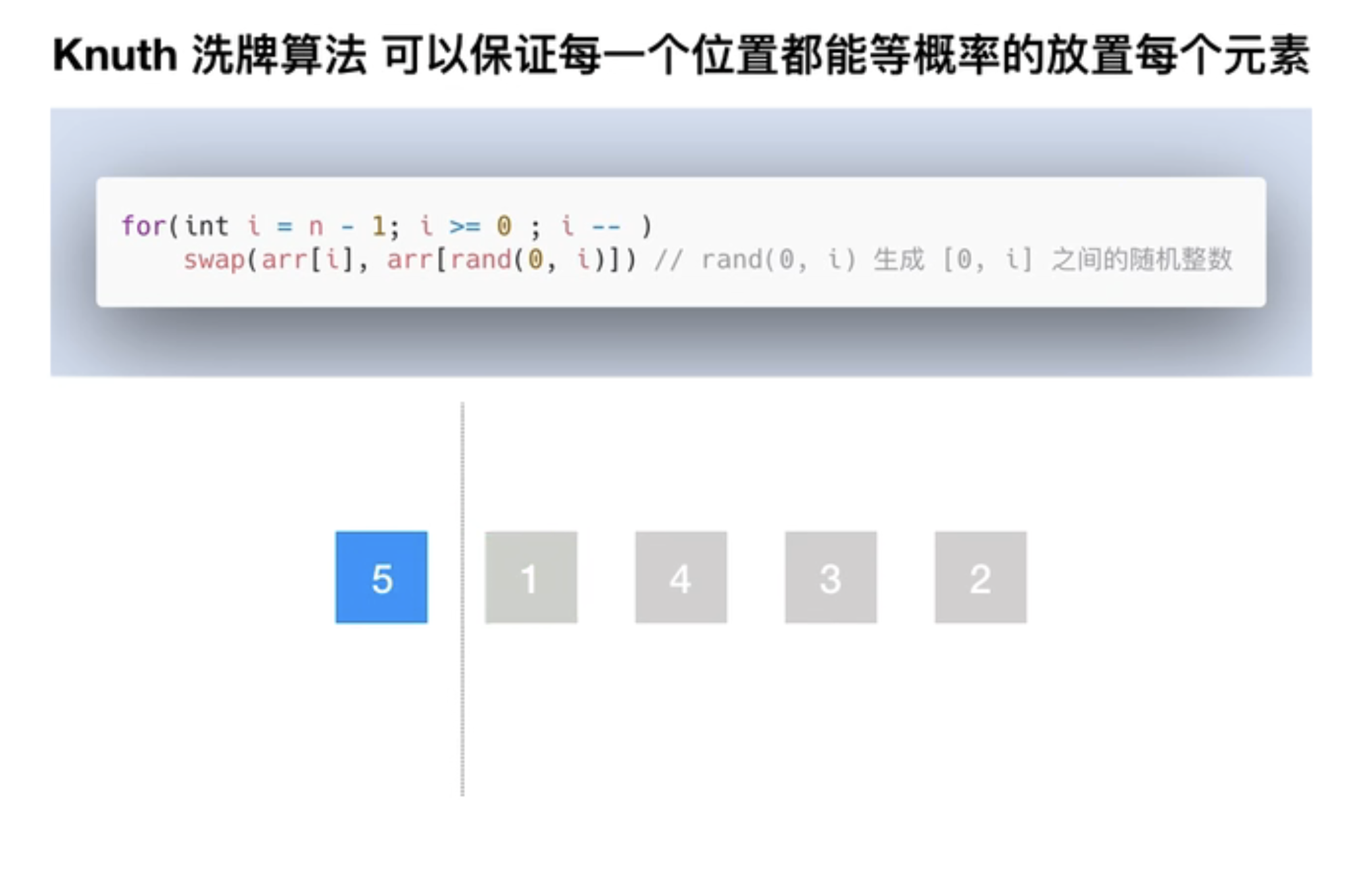
假设有N个数据（下标则是[0,N-1]），第一步随机从0-N-1的范围里面随便取一个索引（我们从后向前面处理），并将这个索引的值交换到N-1这个下标上。这个操作中，每个数被取到的概率都是均等的。经过这个操作之后，将待处理的数据的规模减 1。

第一步：元素5被选中的概率是1/5

第二步：元素3被选中的概率是4/5 * 1/4 = 1/5（第一轮没有被选中概率是4/5，第二轮被选中，概率是1/4，看不懂的请查看概率论的知识点）

第五步: 元素5被选中的概率是4/5* 3/4 * 2/3 * 1/2 * 1 = 1/5(前面 4 个代表没有被选中的概率，最后一个代表一定会被选中)

不断的重复上述过程，直到处理到数组的第一个元素，则完成了数组的随机化处理，并且保证了数组每个元素被等概率的随机化。

/**
 * 随机化数组
 * @param {number[]} arr 待随机化数组
 */
function shuffle(arr) {
  for (let i = arr.length - 1; i >= 0; i--) {
    // 因为JS的随机数范围是[0, 1)，对其取floor之后，随机数范围则变成了[0, i - 1]， 所以为了保证，每个数都有机会被选取到，生成随机索引时，要传入i+1，
    // 使得生成的随机数索引范围在[0, i]之间
    const rndIdx = Math.floor(Math.random() * (i + 1));
    // 将随机选中的数交换到当前处理的位置上
    let tmp = arr[i];
    arr[i] = arr[rndIdx];
    arr[rndIdx] = tmp;
    // 完成交换之后，数据规模递减，直到完成所有的处理
  }
}

DANGER

需要注意的就是JS的随机数的范围是[0, 1)的半闭半开区间，在经过Math.floor处理之后，注意需要保证能够把当前正在处理的位置上的元素有概率选进去，否则就不是真正的随机化了。