递归

1、基本概念

递归（recursion）：指的是函数自己调用自己的过程。在递归中，一个函数通过调用自身来解决更小的子问题，然后将这些子问题的结果组合起来解决更大的问题，直到得到最终结果。

递归函数通常包含两个部分：递归基（base case）和递归关系（recurrence relation）。

递归基是递归函数的基本结束条件，当满足递归基条件时，递归函数不再调用自身，直接返回一个结果，终止递归。

递归关系则是递归函数的递推式，它描述了如何将原问题分解成更小的子问题，并将它们组合起来解决原问题。在递归函数的每一层递归中，递归关系都会被调用一次或多次，直到达到递归基的条件。

递归通常应用于问题的分治或分解，通过将大问题分解成小问题来简化问题的求解。在实际应用中，递归可以实现数据结构的遍历、搜索、排序等算法。

递归的一个显著特征就是简单，这就是为什么我在上述介绍中将递推式三个字加粗的原因，只要能够找到一个递推式，把一个大问题规模减小，小问题化了的办法就能使用递归，但是简单归简单，带来的问题就是递归的函数体占用的内存规模会随着递归深度的增加而增加。每次递归调用都需要在内存中保存当前函数执行状态的上下文信息，包括函数参数、局部变量、返回地址等，这些信息都需要在内存中占用一定的空间。如果递归深度过大，那么就会占用大量的内存空间。

递归的本质是利用函数的调用栈实现的，因为系统堆栈的长度是有限的，如果一旦出现递归的调用深度过长，那么就会出现爆栈的错误。

下图是表示求斐波拉契数列中第4项，系统堆栈调用的关系：

/* 求斐波拉契数列的第N项的值 */
function F(n: number) {
  if (n === 1 || n === 2) {
    return 1;
  } else {
    return F(n - 1) + F(n - 2);
  }
}

所以，可以得到我个人得出的一个简单结论就是，异步函数的递归调用，递归本质上转化成为了对队列的操作，而同步函数的递归调用才是真正在堆栈上的操作。

2、JS的递归

由于JS是基于单线程的，因此它对于异步处理是基于事件轮循来处理的，因此，在JS中的递归就变得有点儿不一样了。

function test(i) {
  requestAnimationFrame(() => {
    console.log(i++);
    test(i);
  });
}

像上述这段代码，你不能说它不是递归吧，但是你如果把它执行了，浏览器还是正常能够响应各类操作。

但是下面这段代码，一旦执行马上就会报最大堆栈调用的错误。

function test2(i) {
  console.log(i++);
  test2(i);
}

为什么两个都是递归调用，但是表现出来的行为却完全不一致呢？这就需要我们对JS的事件轮循有足够深的认识了。

前文中提到的调用栈，其实你可以把它理解为它是在一个执行上下文中的（这是我自己的理解，非官方阐述），如果你一直往这个栈里面增加内容，在有限的栈长度下，最终肯定会爆栈。

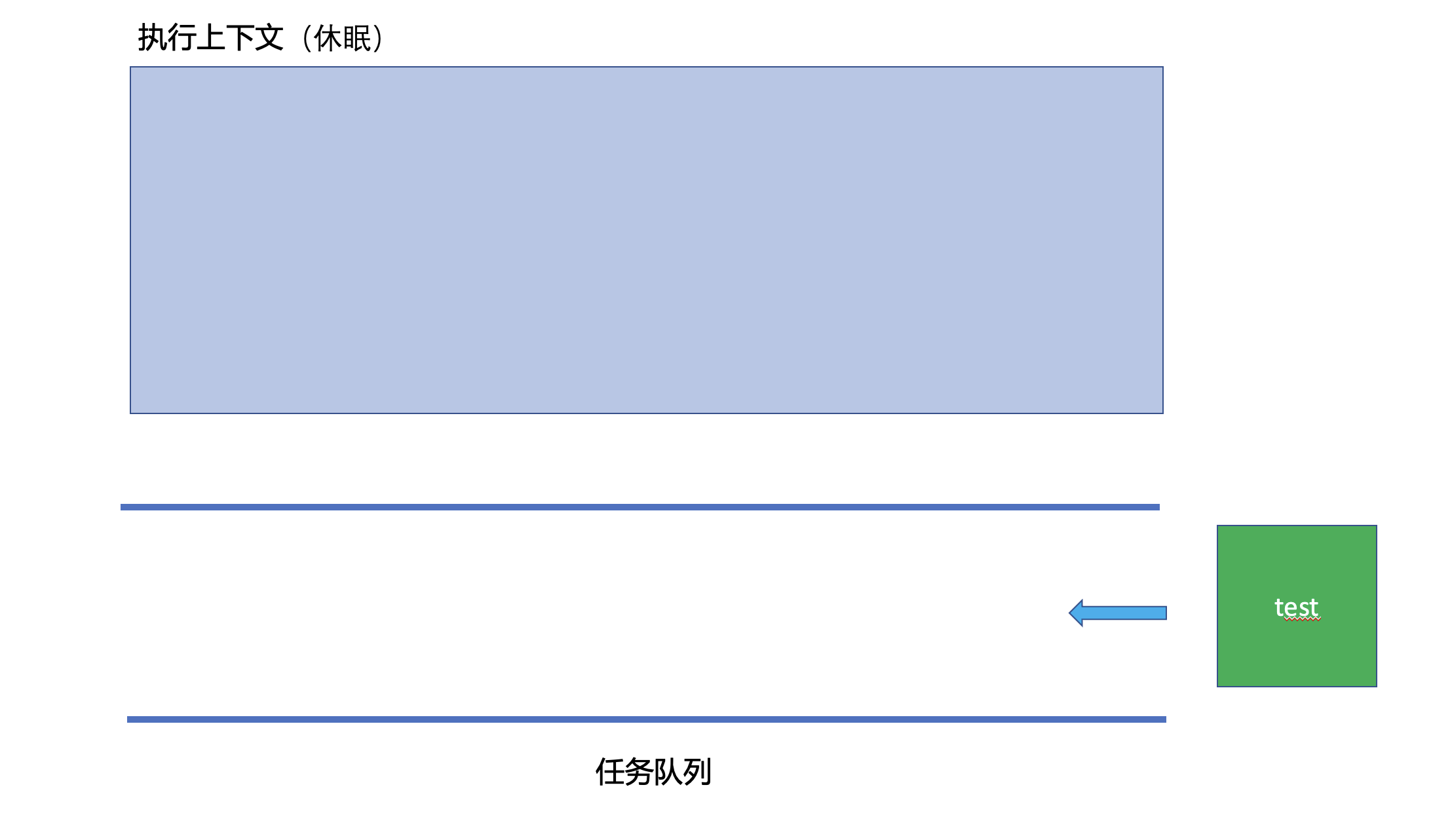
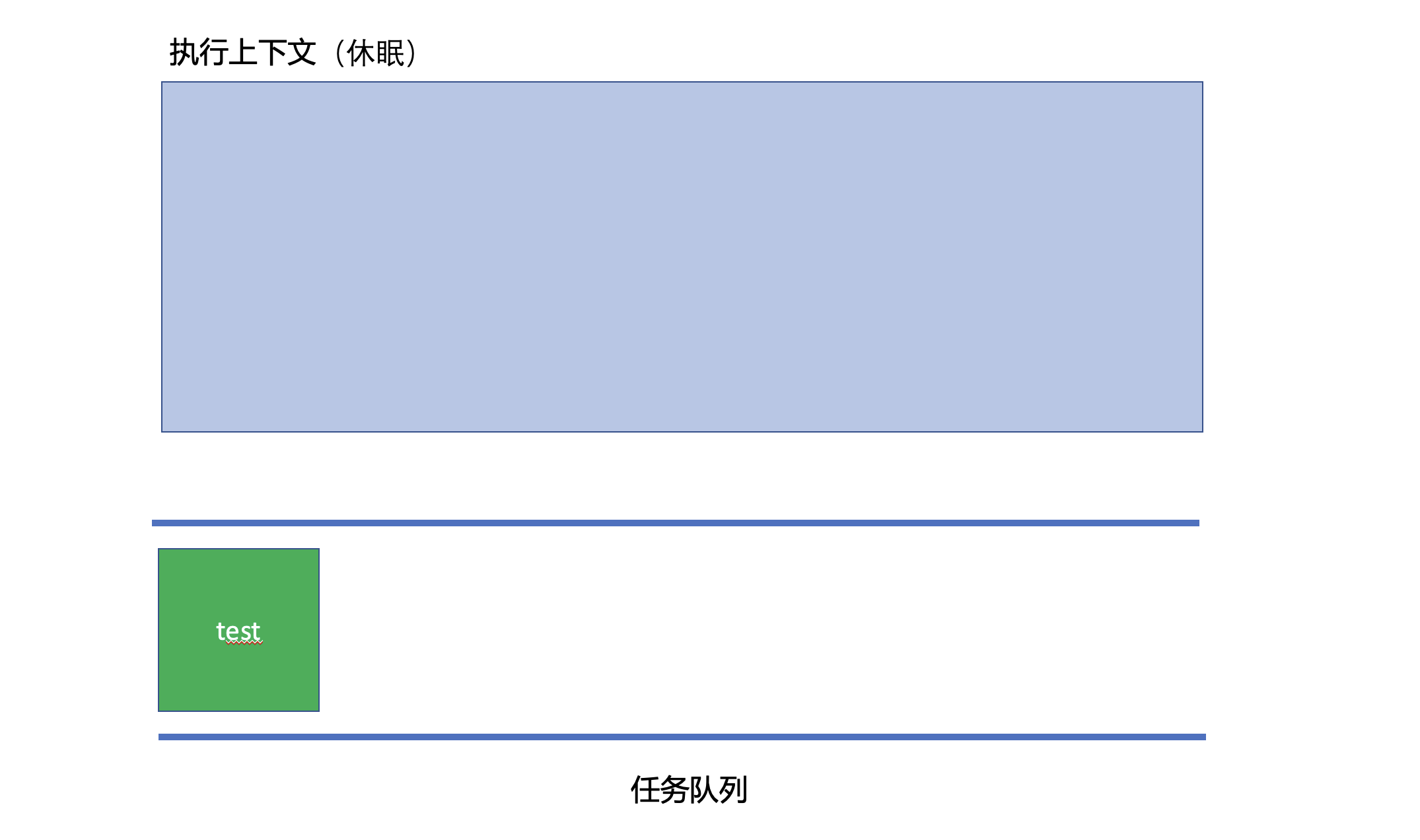
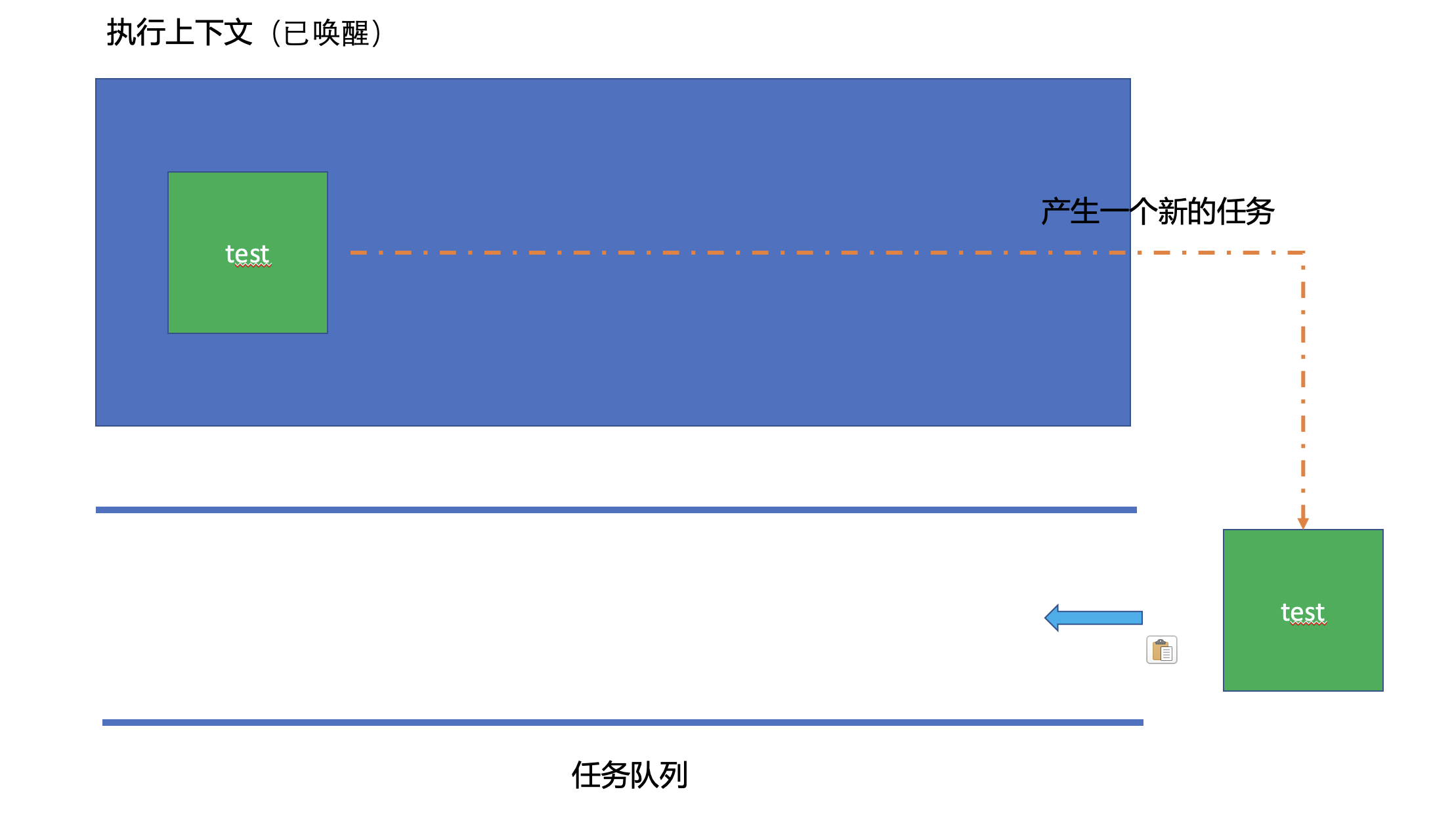
但是基于requestAnimationFrame的递归调用，其实它的执行流程是这样的，JS其实是有一个任务队列（其实有很多个任务队列，如微任务队列，定时任务队列等，我们在讨论这个地方时候可以不用关心那么多队列，所以就只讨论一个任务队列就好），首先如果这个任务队列中没有任务，那么JS主线程就休眠，当这个认为队列里面有内容的时候，JS主线程就取消休眠，并且从任务队列中取出一个任务来处理（这就是所谓的同步任务），但是，一个同步任务中，又有可能加入新的任务到任务队列中去，之前的requestAnimationFrame函数内递归调用了test函数，就产生了一个新的任务追加到了任务队列里面去，所以，这个递归操作其实导致的结果，是使得JS的主线程每时每刻都有活儿干，而并不会产生最大堆栈调用的错误。

这个特性是JS语言本身的特性，开发者需要尤为注意。

以下是test函数的执行流程：

3、递归的优化

对于递归中一个比较重要的优化就是缓存结果，回到我们开始所阐述的利用递归求斐波拉契数列的问题，求F(4)，需要先求出F(3)和F(2)，求F(3)需要先求出F(2)和F(1)，在求F(4)的时候，已经有一个F(2)已经在栈内了，但是此时又有一个F(2)要入栈，明显F(2)是被计算了 2 次了（而F(1)被重复计算的次数更多），显然这是浪费了时间的。

因此，我们可以在计算的过程中将计算结果缓存下来，避免重复的递归。

所以，上述斐波拉契数列的求解方法可以优化为如下代码：

function F(n: number) {
  return _fibonacci(n, new Map());
}

function _fibonacci(n: number, map: Map<number, number>) {
  if (typeof map.get(n) !== "undefined") {
    return map.get(n);
  } else if (n === 1 || n === 2) {
    map.set(n, 1);
    return 1;
  } else {
    const last = _fibonacci(n - 1, map);
    // 注意，这个地方不能写到F(n - 2, map)后面，否则仍然会产生重复计算
    map.set(n - 1, last);
    const preLast = _fibonacci(n - 2, map);
    map.set(n - 2, preLast);
    return last + preLast;
  }
}

可以用这两版本的实现分别比较一下执行时间：

export function F1(n: number) {
  if (n === 1 || n === 2) {
    return 1;
  } else {
    return F1(n - 1) + F1(n - 2);
  }
}

export function F2(n: number) {
  return _fibonacci(n, new Map());
}

function _fibonacci(n: number, map: Map<number, number>) {
  if (typeof map.get(n) !== "undefined") {
    return map.get(n);
  } else if (n === 1 || n === 2) {
    map.set(n, 1);
    return 1;
  } else {
    const last = _fibonacci(n - 1, map);
    // 注意，这个地方不能写到F(n - 2, map)后面，否则仍然会产生重复计算
    map.set(n - 1, last);
    const preLast = _fibonacci(n - 2, map);
    map.set(n - 2, preLast);
    return last + preLast;
  }
}

测试文件：

import { F1, F2 } from "./recursion";

describe("fibonacci", () => {
  it("recursion", () => {
    let now = Date.now();
    const f1 = F1(34);
    console.log(Date.now() - now);
    now = Date.now();
    console.log(f1);
    const f2 = F2(34);
    console.log(Date.now() - now);
    console.log(f2);
  });
});

F1的执行时间为120ms，F2的执行时间为3ms，不同电脑的执行时间可能会有差异，但是这是一个能够明显感知到差异的优化。

第二个要说的优化点是尾递归优化，在说这个优化之前，先明确一下什么是尾递归调用

尾递归调用指的是一个递归函数中，递归调用出现在函数的最后一行。也就是说，在函数执行完最后一步后，只有递归调用返回的结果被用到，而函数本身并没有执行其他操作。这种情况下，可以对递归调用进行优化，避免调用栈的不必要增长，从而提高程序的性能。尾递归优化通常会将递归转换成循环，避免了每次递归调用都需要在栈上分配空间的开销。

比如，一个用递归实现的求和函数：

不用尾递归，是这样的：

function sum(n: number) {
  if (n === 0) {
    return n;
  } else {
    return n + sum(n - 1);
  }
}

使用了尾递归优化之后，可以将sum改写成这样：

function sum(n: number, acc: number) {
  if (n === 0) {
    return acc;
  } else {
    return sum(n - 1, acc + n);
  }
}

据说V8引擎是支持尾递归优化的，但是我一次都没有尝试成功 😂，如果上述这个经过优化的函数拿到NodeJS或浏览器下跑，表现的行为和未优化的函数一致。

除此之外，别的优化方式就是改变算法的实现方式了，比如递归转迭代，递归转动态规划等手段。

虽然说递归有它的不足，但是在实际的编码中也不要一用到递归就会觉得可能有爆栈的风险，还是有取决于你的数据量，不要过早的优化，毕竟递归的实现逻辑相对简单，代码可读性高，因此需要辩证的看待递归。