AVL 树

AVL树是一颗自平衡二叉搜索树。在AVL树中任何节点的两个子树的高度最大差为 1，所以它也被称为高度平衡树。增加和删除可能需要通过一次或多次树旋转来重新平衡这个树。AVL树得名于它的发明者G. M. Adelson-Velsky和E. M. Landis。

在阅读本文之前，请确保你已熟知二叉搜索树。

AVL 树的节点定义

因为AVL树需要根据树高对树进行平衡性的调整，所以在树的节点上需要增加一个height域。

/**
 * AVL树节点
 */
interface AVLTreeNode<T> {
  /**
   * 左子树
   */
  left: AVLTreeNode<T> | null;
  /**
   * 右子树
   */
  right: AVLTreeNode<T> | null;
  /**
   * 节点值
   */
  val: T;
  /**
   * 树高
   */
  height: number;
}

AVL 树的旋转

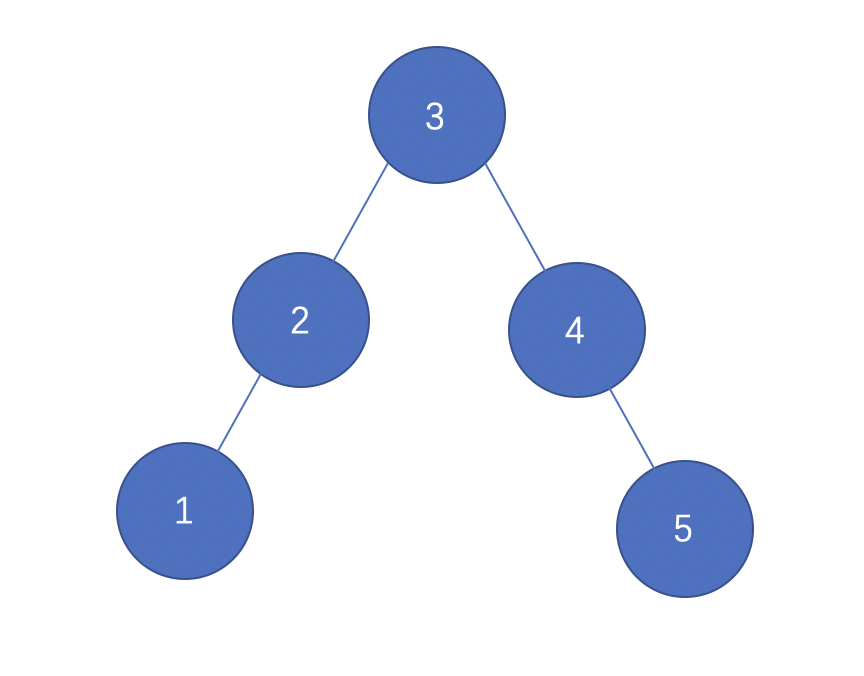
在上文我们提到在AVL树中，任何节点的两个子树的高度最大差为 1，那么，其实除开左子树或右子树上多出来的那个节点（后文我们就把它称之为孤儿节点，上图中值为 1 的节点，或值为 5 的节点），别的部分也是平衡的；

如红框里圈出来的：

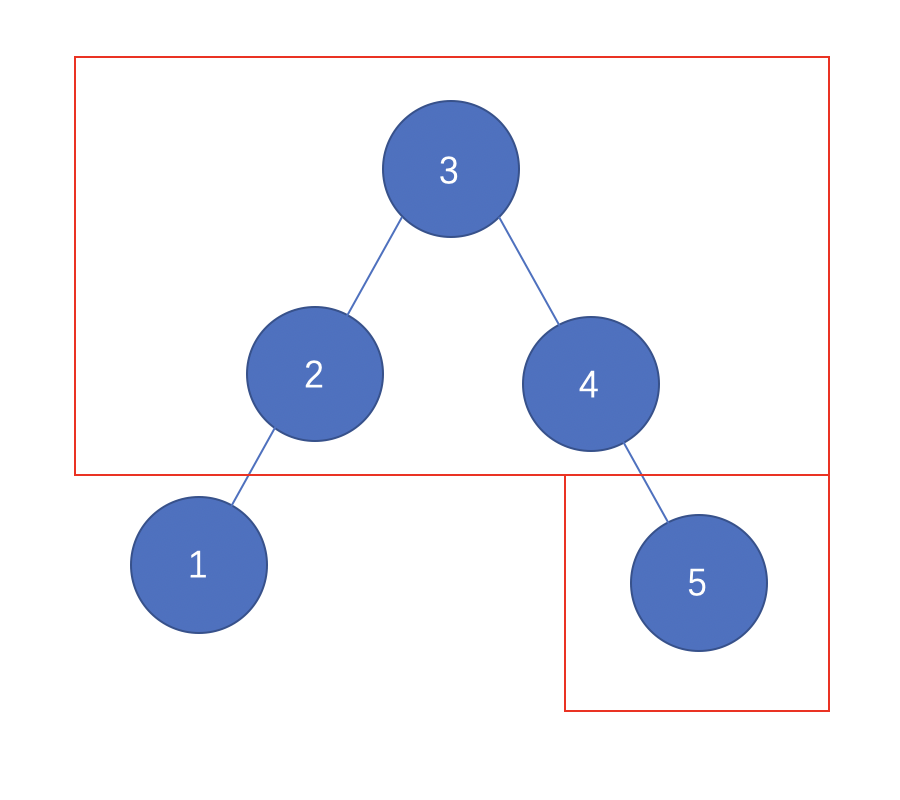
对于节点 3，左子树高度 1，右子树高度 2，平衡因子 -1；

对于节点 2，左子树高度 0，右子树高度 0，平衡因子 0；

对于节点 4，左子树高度 0，右子树高度 1，平衡因子 1；

对于节点 5，左右子树高度 0，平衡因子 0；

因此，为了便于理解后面的几个旋转，我们就可以把问题抽象成这样：

孤儿节点为左子结点：

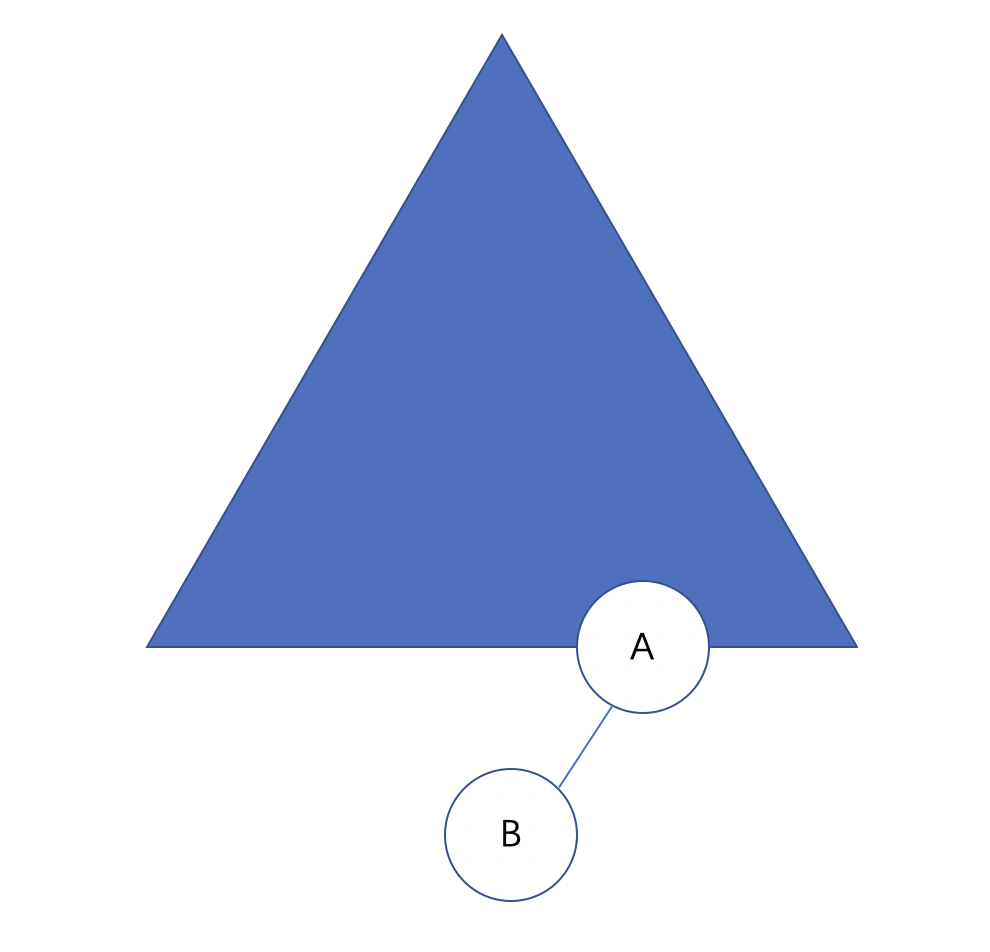
孤儿节点为右子结点：

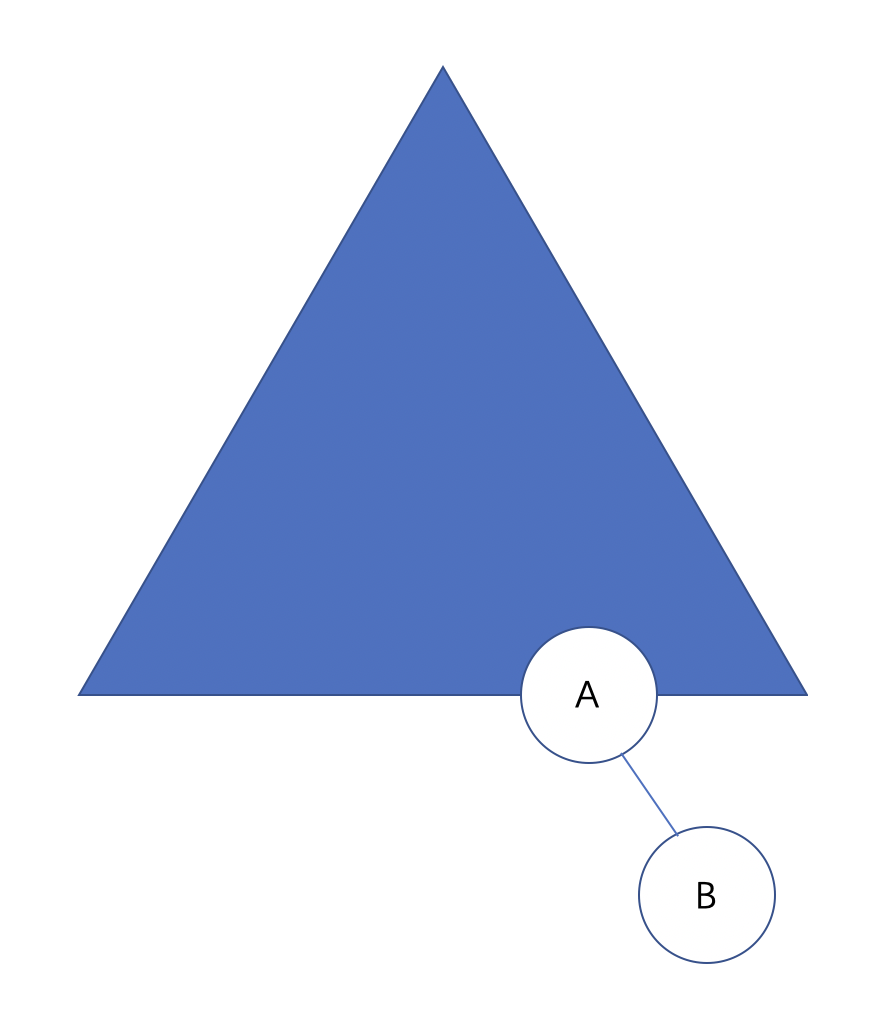
LL 旋转

若孤儿节点为左子节点（L），在其左子结点(L)上插入 C子树（还是因为任何节点的两个子树的高度最大差为 1的特征，C是可以有子节点的，后续不再赘述）：

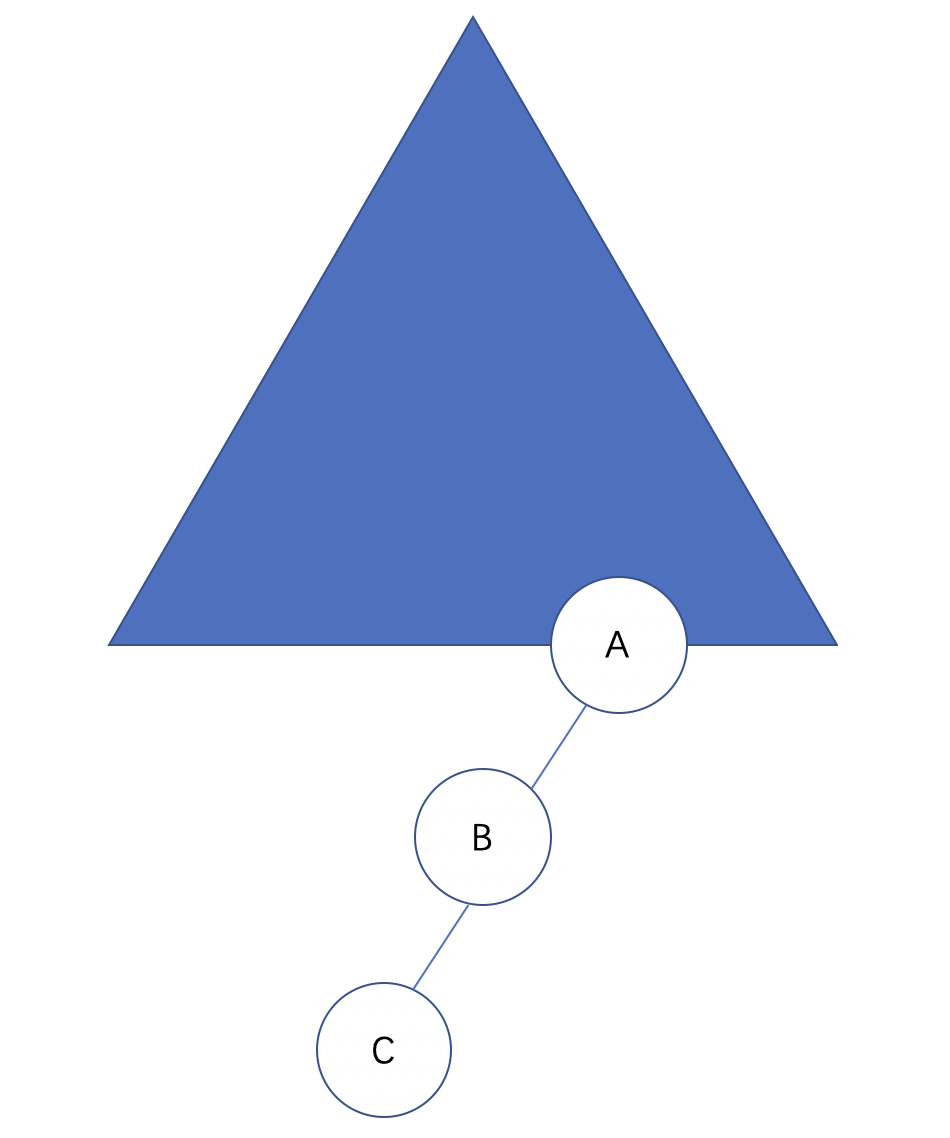
对于节点A，左子树的高度为 2，右子树高度为 0，平衡因子为-2，节点B的左子树高度 1，右子树 0，平衡因子-1；节点C的左右子树都是 0，平衡因子 0。

那么，我们只需要把它调整为CBA的顺序即可。即：

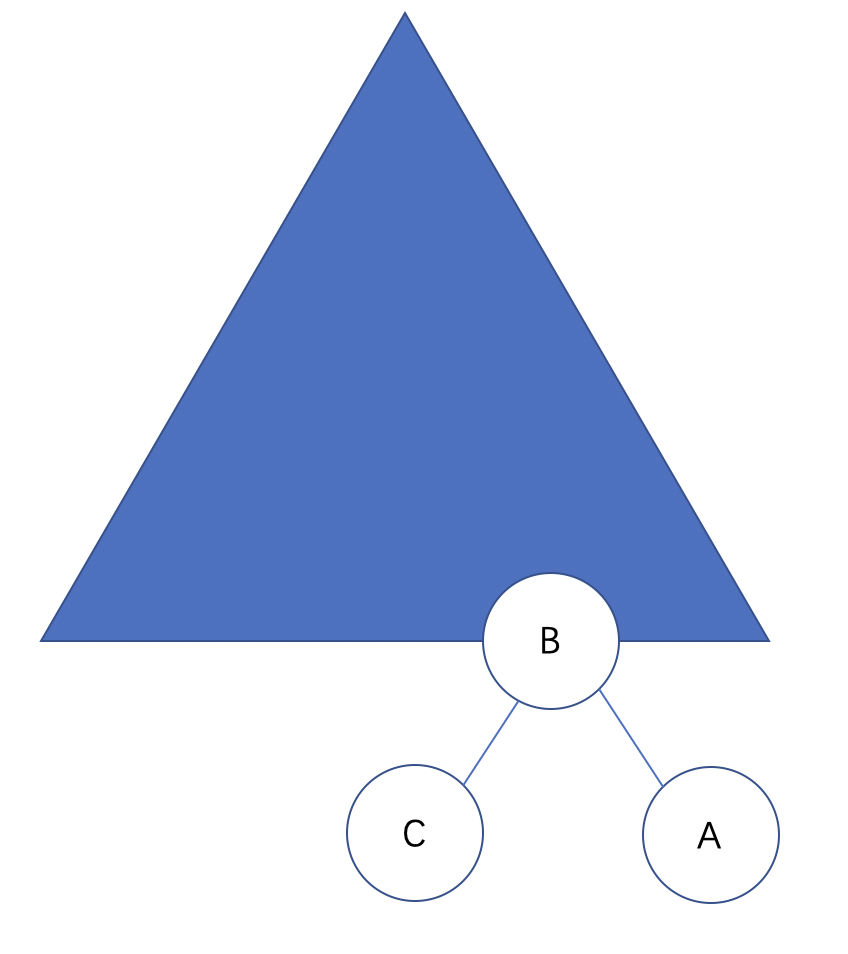
这就是LL旋转，即右旋。因为节点A也可能有右子树，B节点也可能有右子树。那么，B节点的右子树是要比A节点的右子树小的，所以A节点的右子树保持不动，将B的右子树挂在A节点的左子树上，若 C有左右子节点，则保持不动即可。

即：

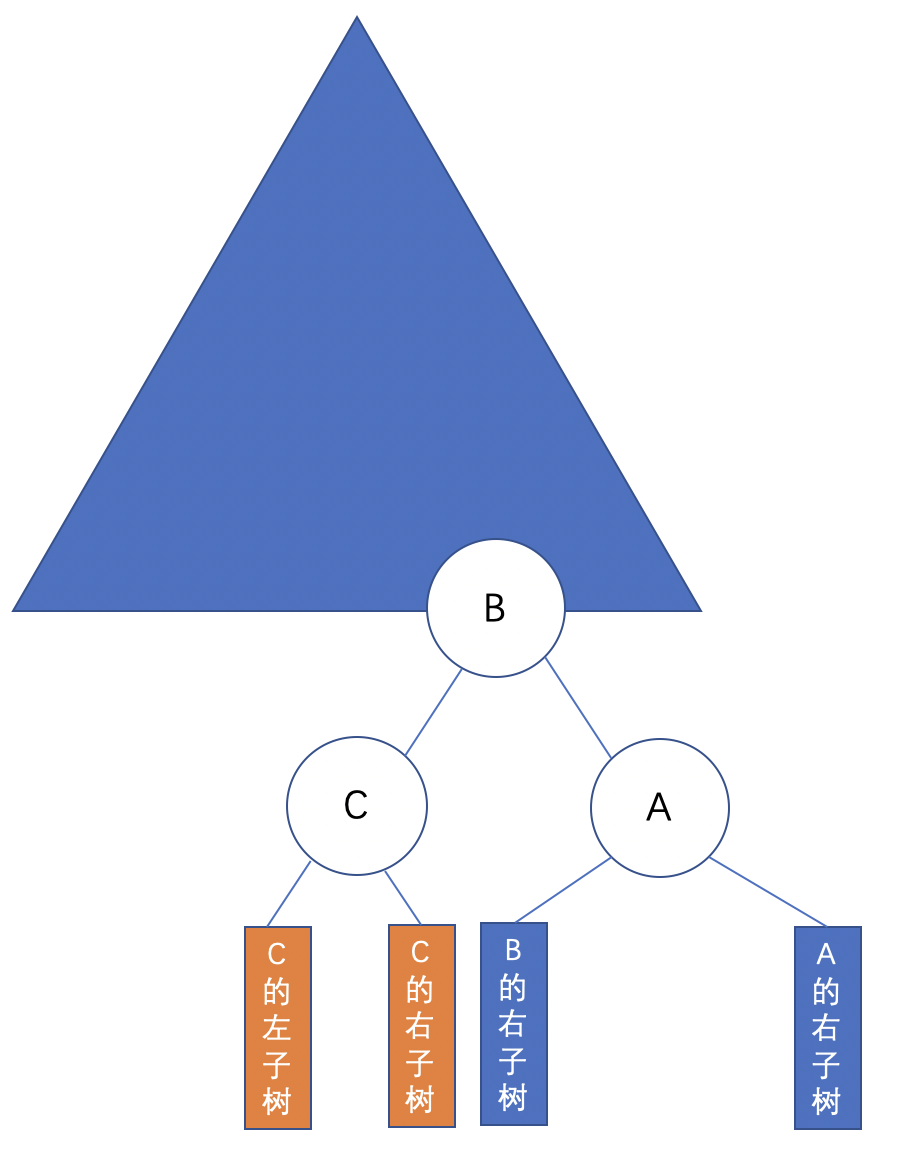
RR 旋转：

若孤儿节点为右子节点（R），在其右子结点(R)上插入 C子树：

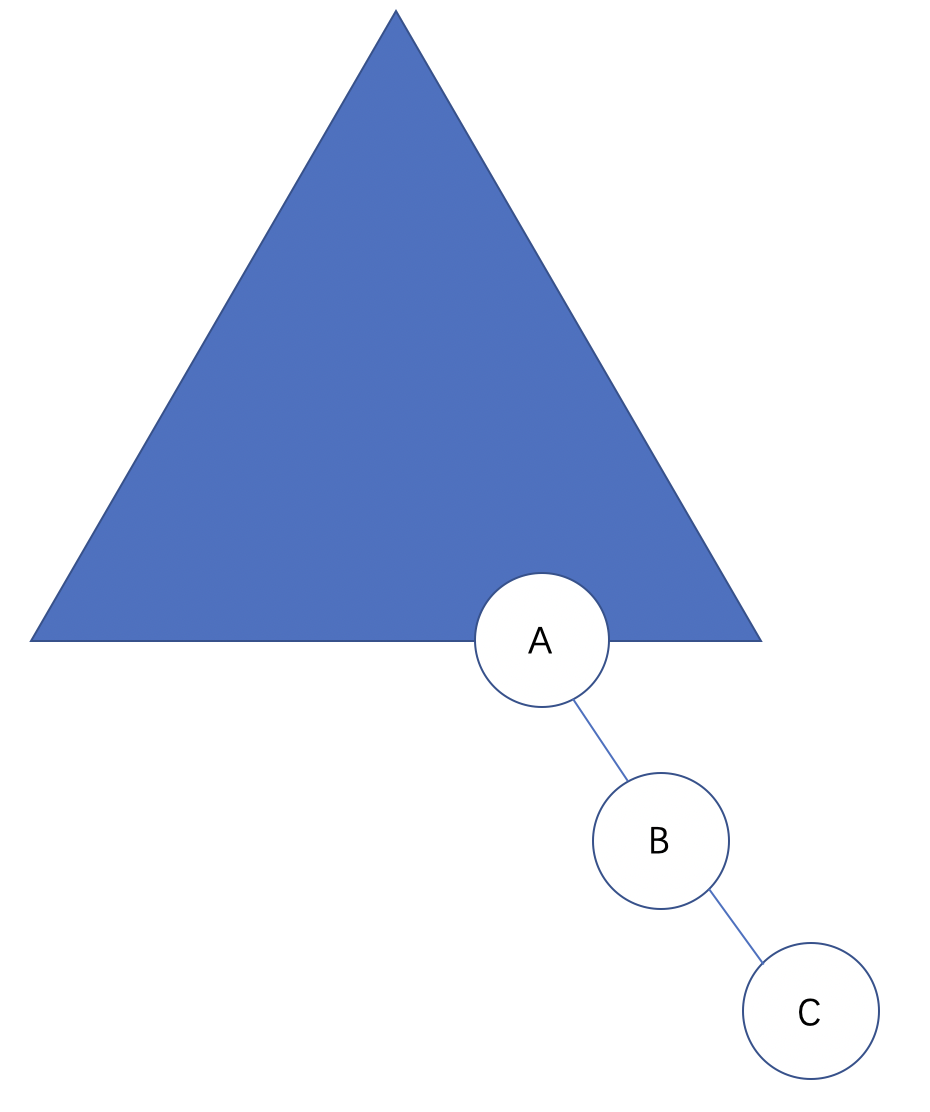
对于节点A，左子树的高度为 0，右子树高度为 2，平衡因子为 2，节点B的左子树高度 0，右子树 1，平衡因子 1；节点C的左右子树都是 0，平衡因子 0。

那么，我们只需要把它调整为ABC的顺序即可。即：

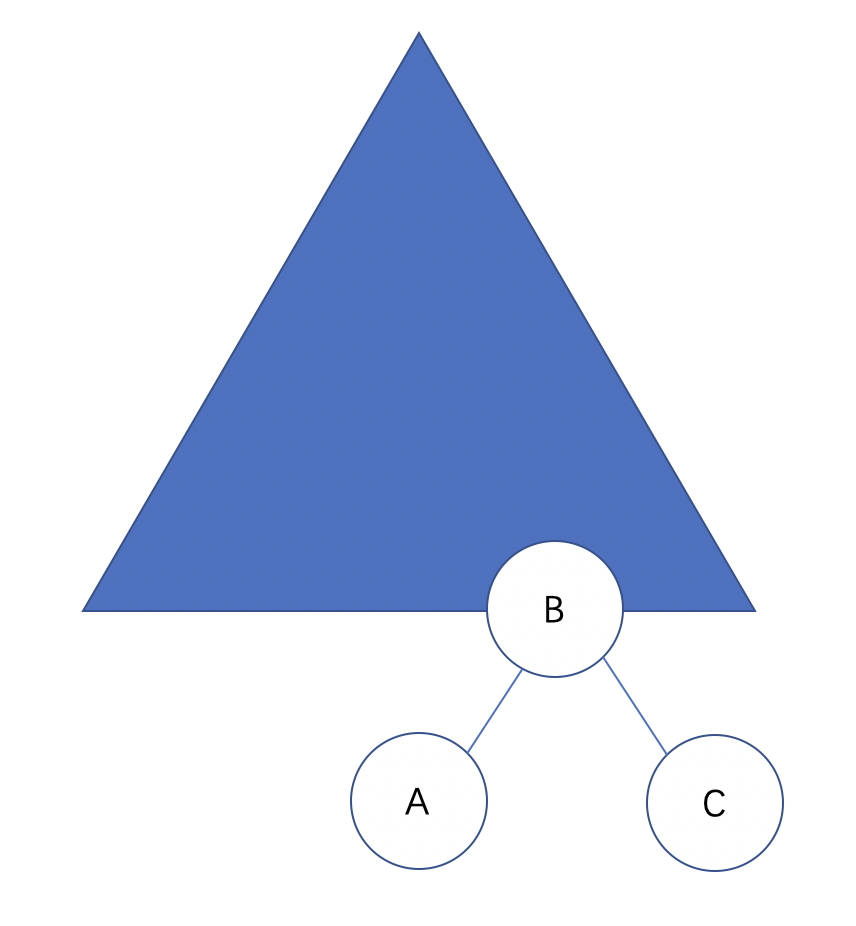
这就是RR旋转，即左旋。因为节点A也可能有左子树，B节点也可能有左子树。那么，B节点的左子树是要比A节点的左子树大的，所以A节点的左子树保持不动，将B的左子树挂在A节点的右子树上，若C有左右子树，则保持不动即可。

即：

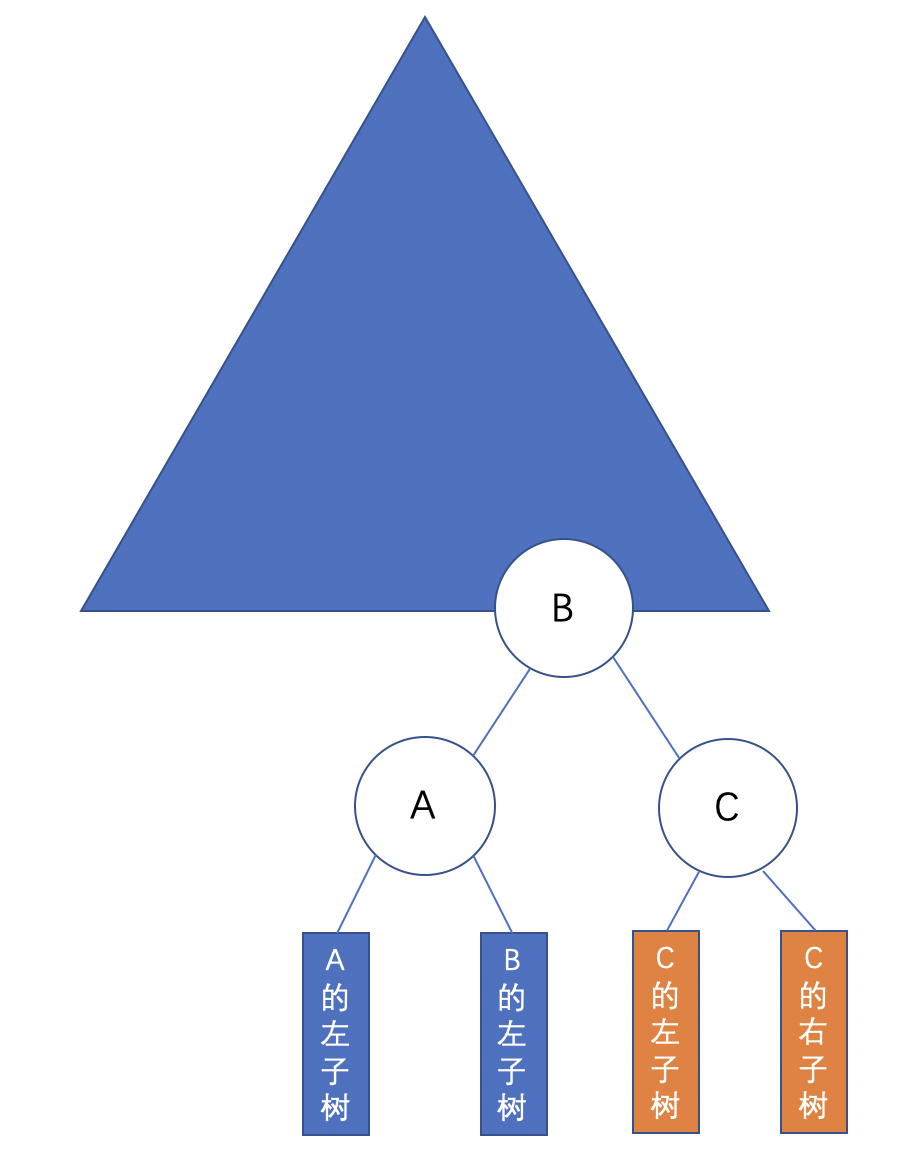
LR 旋转

若孤儿节点为左子节点（L），在其右子结点(R)上插入 C子树：

对于节点A，左子树的高度为 2，右子树高度为 0，平衡因子为-2，节点B的左子树高度 0，右子树 1，平衡因子 1；节点C的左右子树都是 0，平衡因子 0。

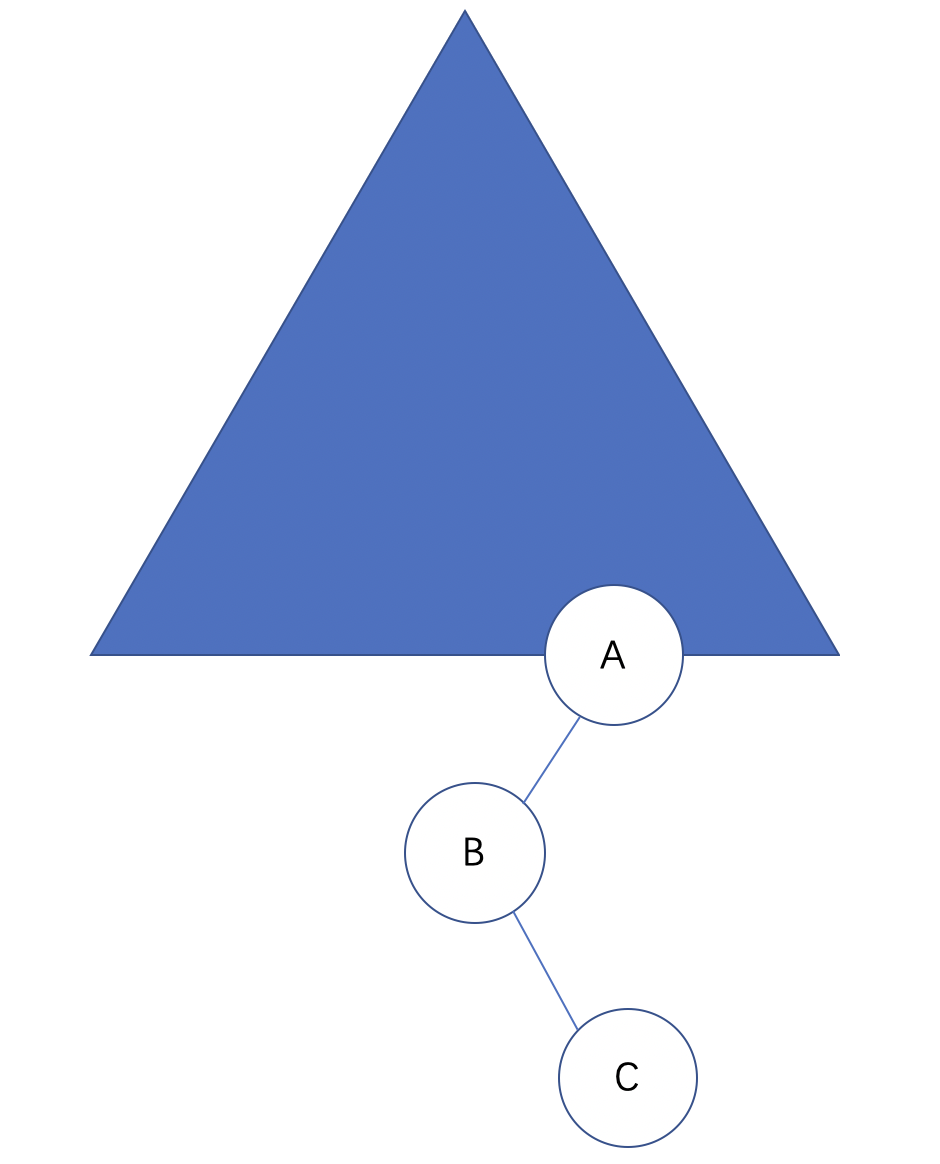
我们需要把它调整为CBA的顺序。

那么，首先得把C提节点上去，即：

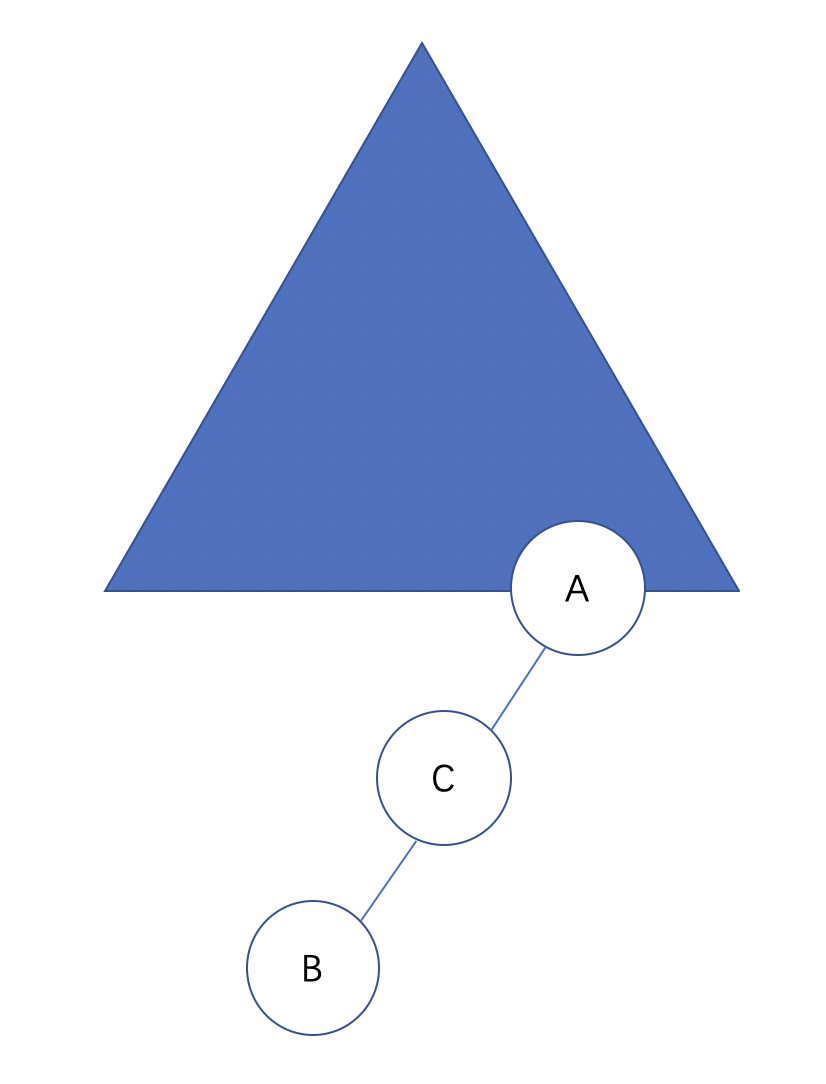
接着，我们把C再次向上提，把A往右下压，即：

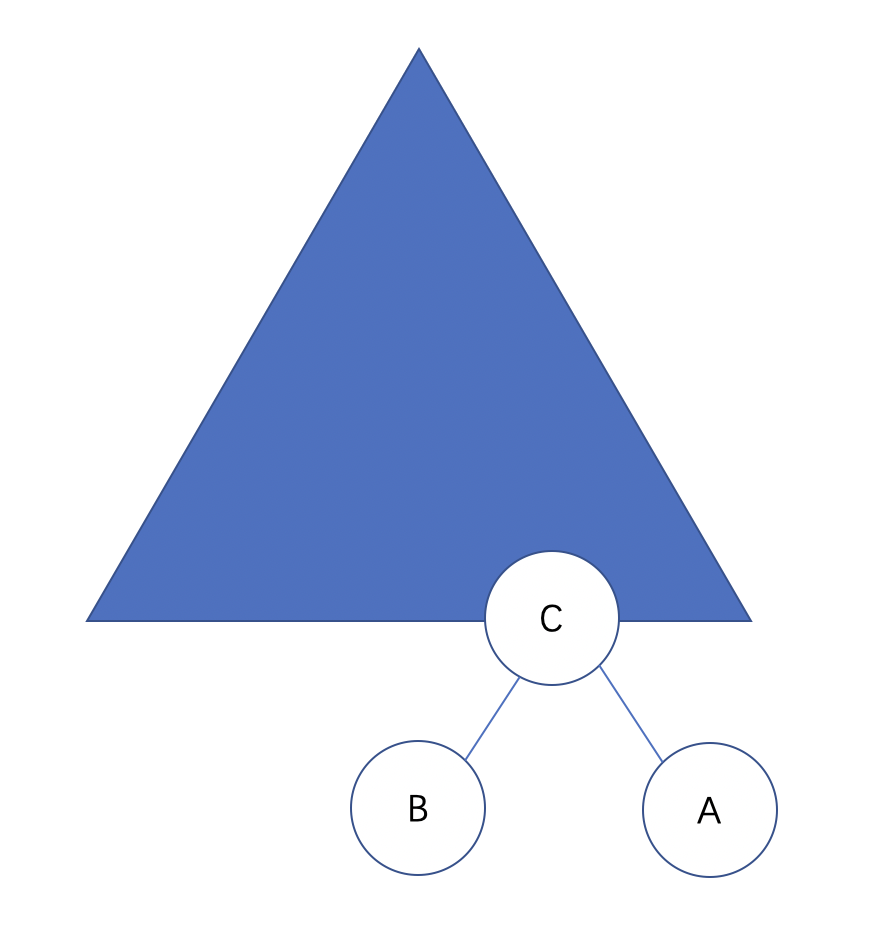
同理，上述情况节点A可能有右子树，节点B可能有左子树，其实是保持不变的，但若C有左右子树，可以确定的是C的左右子树都是小于A的，C 的左右子树都是大于B的，那么C的左子树可以放在B的右子树上，C的右子树可以放在A的左子树上，即：

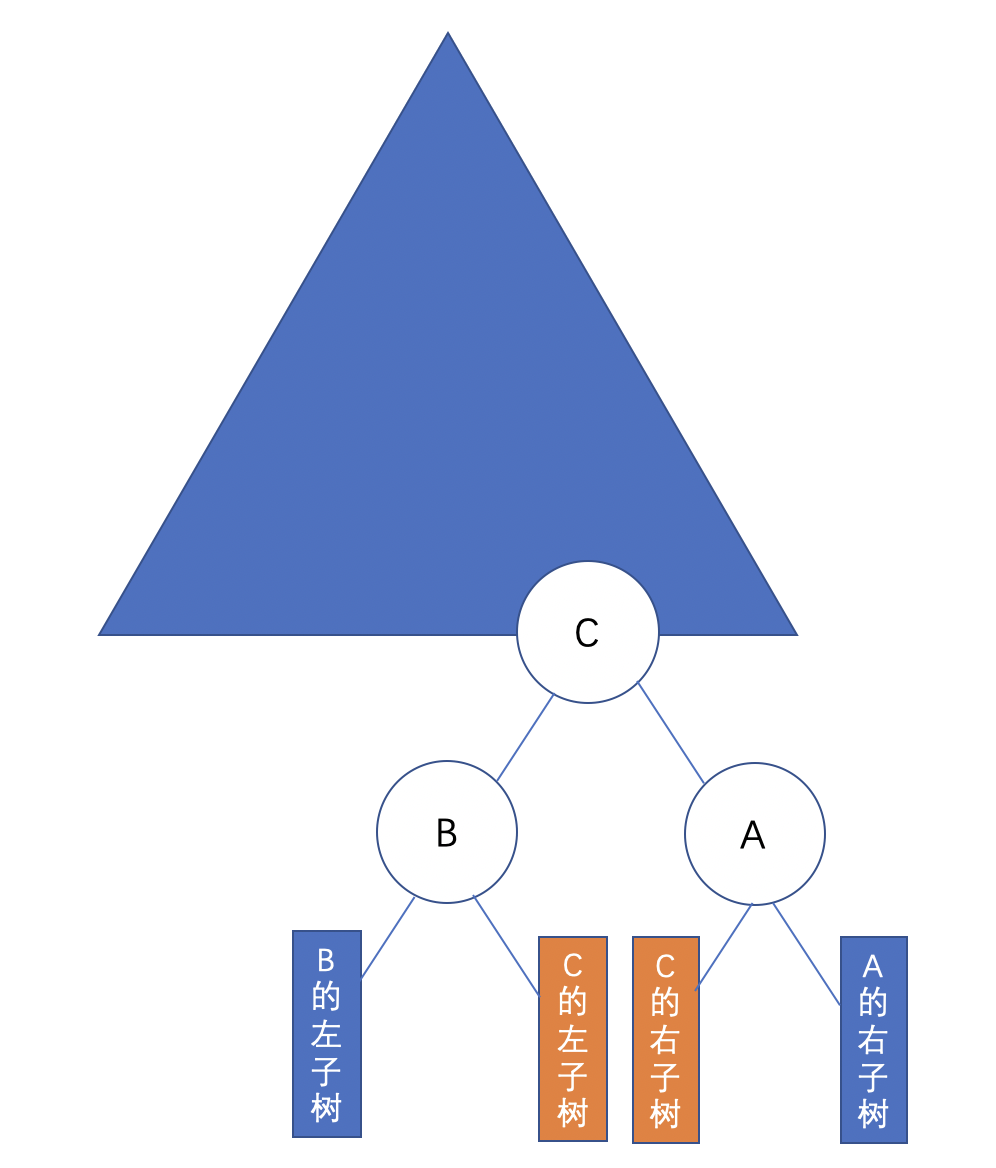
可以看到，LR旋转，是先对节点 B进行了一次RR旋转（先左旋），再对 A 进行一次LL旋转（再右旋）。

RL 旋转

若孤儿节点为右子节点（R），在其左子结点(L)上插入 C子树：

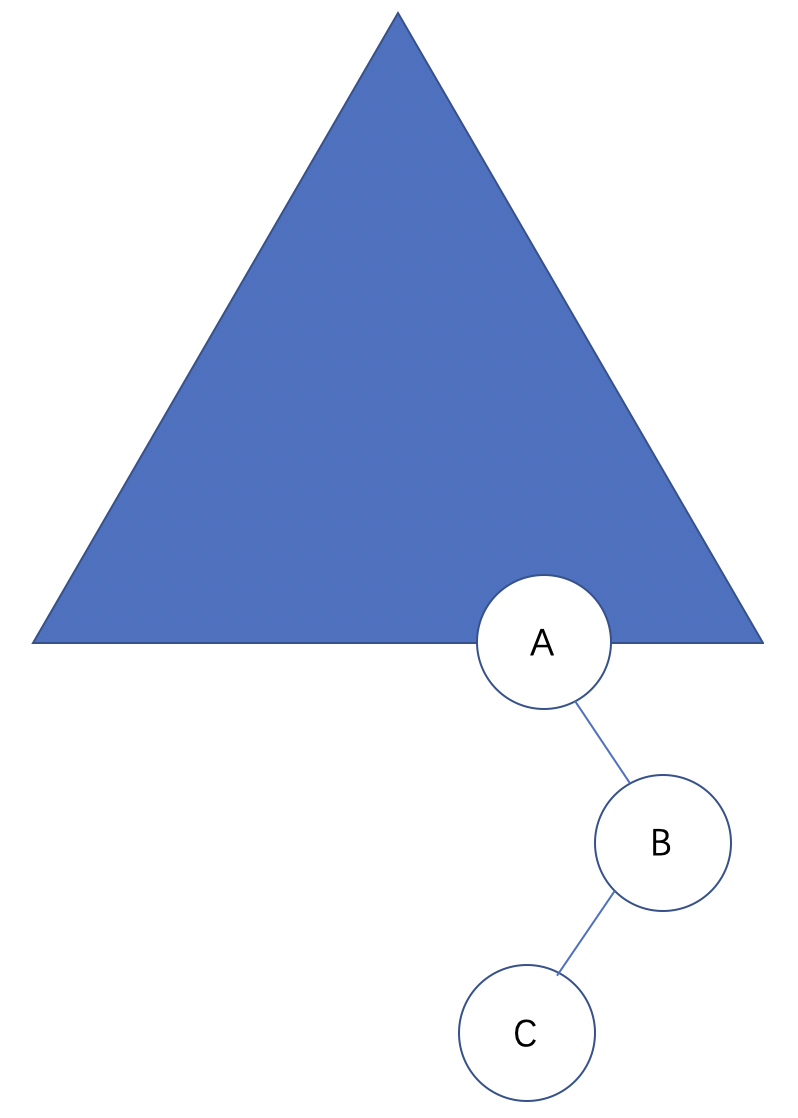
对于节点A，右子树的高度为 2，左子树高度为 0，平衡因子为 2，节点B的左子树高度 1，右子树 0，平衡因子 -1；节点C的左右子树都是 0，平衡因子 0。

我们需要把它调整为ACB的顺序。

那么，首先得把C提上去，即：

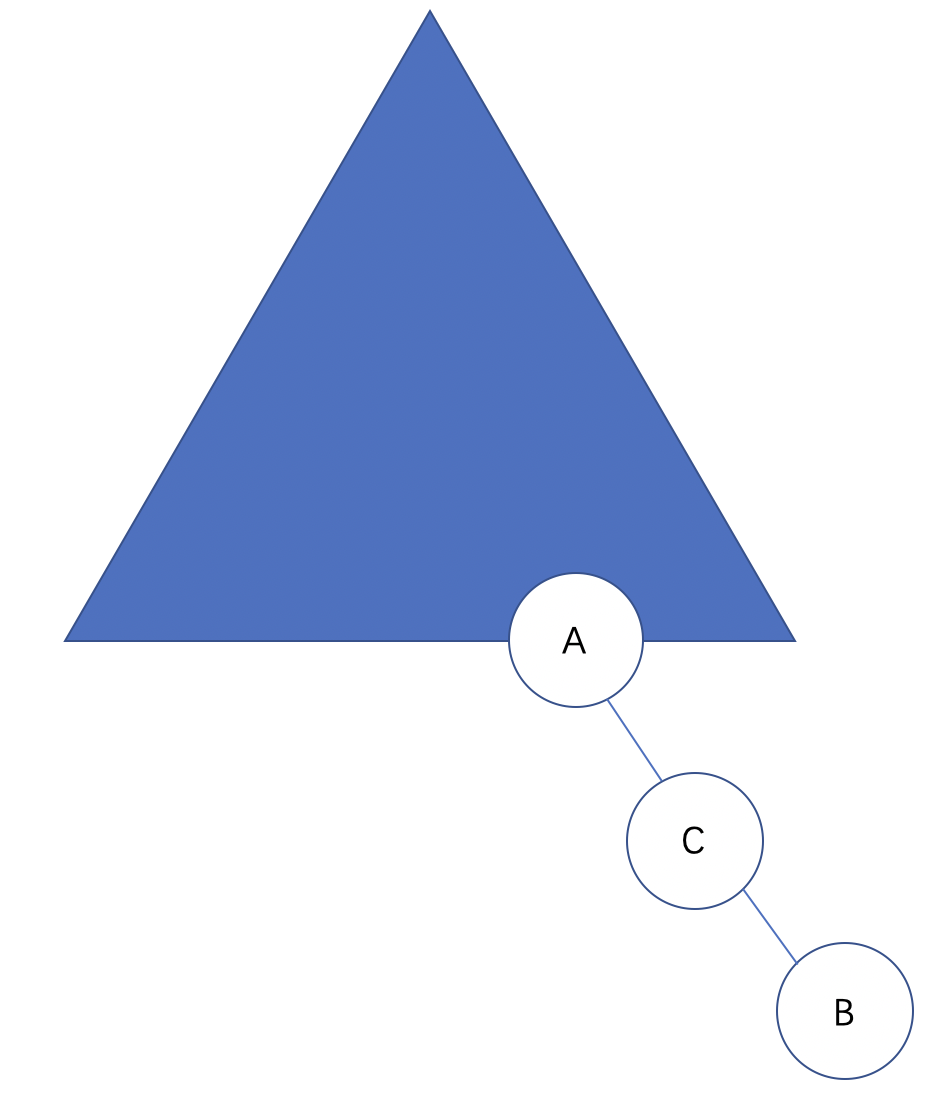
接着，我们把C再次向上提，把A往左下压，即：

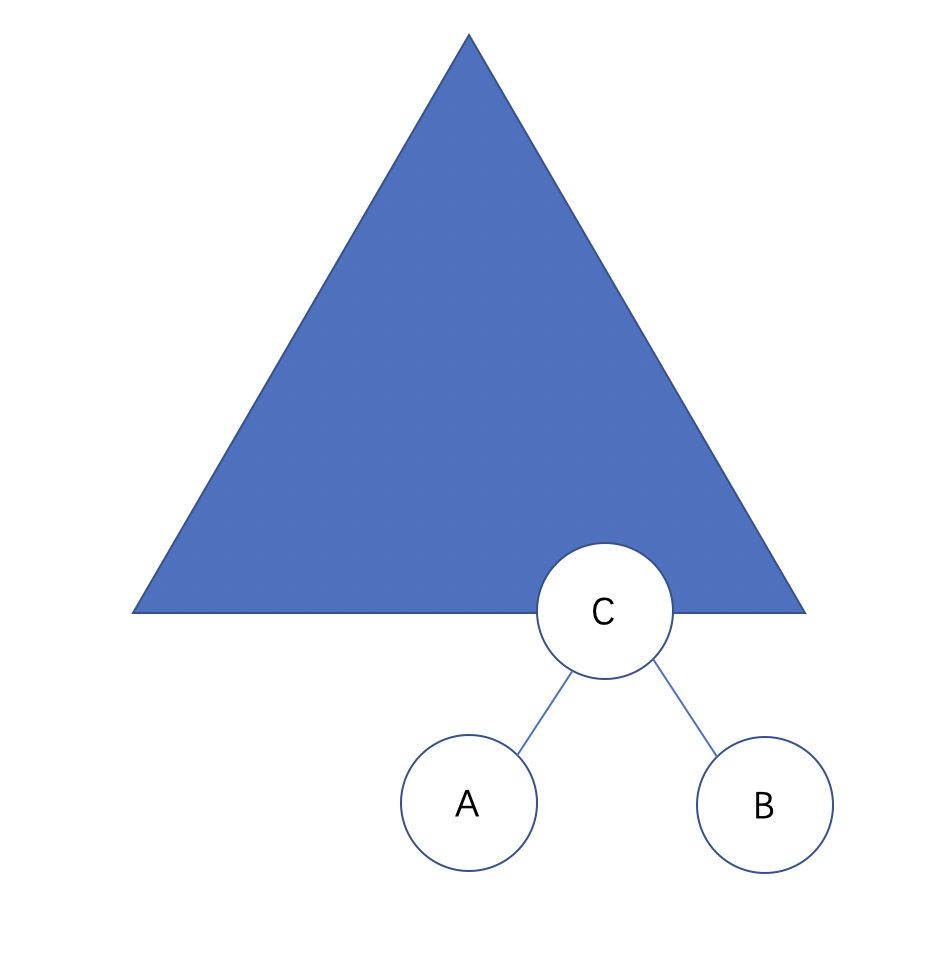
同理，上述情况节点A可能有左子树，节点B可能有右子树，其实是保持不变的，但若C有左右子树，可以确定的是C的左右子树都是大于A的，但C的左子树一定是小于B的，那么C的左子树可以放在B的左子树上，C的右子树可以放在A的右子树上，即：

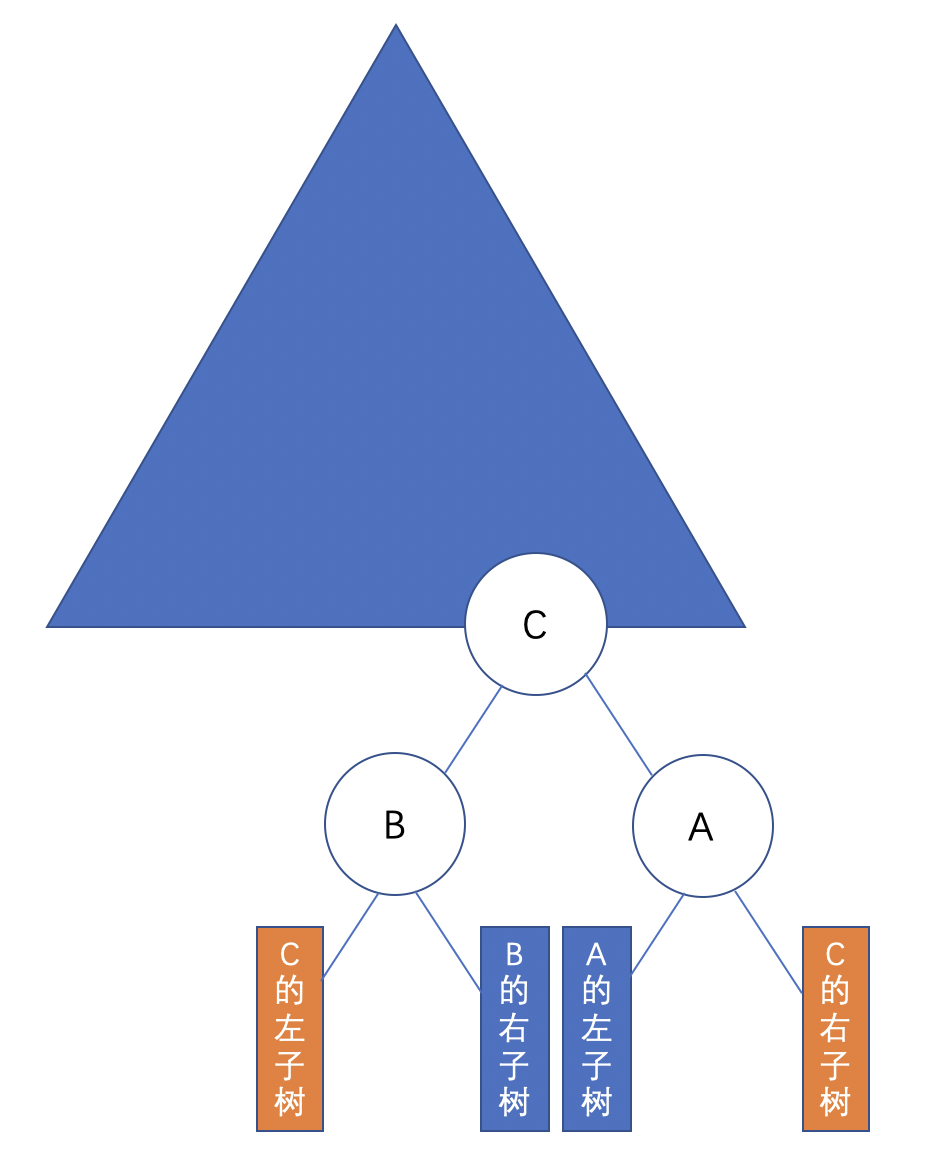
可以看到，RL旋转，是先对节点 B进行了一次LL旋转（先右旋），再对 A 进行一次RR旋转（再左旋）。

这儿有个易混淆的点大家需要关注一下，LL旋转是右旋，RR旋转是左旋，对于LR旋转和RL旋转的旋转过程取决于你怎么解读L和R了，比如你将LR旋转解读为LL旋转+RR旋转，先进行的是RR旋转，再进行LL旋转，如果你将LR旋转解读为左旋和右旋，则先左旋，再右旋。

AVL 树旋转代码的实现

首先定义一个获取树高的辅助函数

/**
 * 获取以treeNode为根节点的树的高度
 * @param {AVLTreeNode<number>} treeNode
 */
function getHeight(treeNode) {
  return treeNode ? treeNode.height : 0;
}

LL 旋转

上面的旋转流程，我们已经阐述的很清楚了，因为是LL旋转，那么A是必须有一个左节点B的（因为我们现在插入的是C子树），把B往右上拽，把A往右下压，然后B成为了新树的根节点，重新更新一下左右子树的高度即可，现在B的左子树是B本来的左子树（即上述流程中的C），B的右子树则是调整之后以A节点为根节点的子树。A节点的左右子树没有变化，重新处理一下它的左右子树即可。

/**
 * LL单旋
 * @param {AVLTreeNode<number>} A
 * @returns {AVLTreeNode<number>}
 */
function singleLeftRotation(A) {
  /* 注意：A必须有一个左子结点B */
  let B = A.left;
  // 注意： 一定要先把B的右子树挂在A的左边
  A.left = B.right;
  B.right = A;
  /* 将A与B做左单旋，更新A与B的高度，返回新的根结点B */
  A.height = Math.max(this.getHeight(A.left), this.getHeight(A.right)) + 1;
  B.height = Math.max(this.getHeight(B.left), this.getHeight(A)) + 1;
  return B;
}

LR 旋转

在上述流程中，我们是先对B和C进行了一次RR旋转，B即A.left，把A-(左)>B-(右)>C变成了A-(左)>C-(左)>B，然后再对A执行一次LL旋转即完成了LR旋转。

/**
 * LR旋转
 * @param {AVLTreeNode<number>} A
 * @returns {AVLTreeNode<number>}
 */
function doubleLeftRightRotation(A) {
  /* 注意：A必须有一个左子结点B，且B必须有一个右子结点C */
  /* 将A、B与C做两次单旋，返回新的根结点C */
  /* 将B与C做右单旋，C被返回 */
  A.left = this.singleRightRotation(A.left);
  /* 将A与C做左单旋，C被返回 */
  return this.singleLeftRotation(A);
}

RR 旋转

流程和LL旋转类似，此处不再赘述。

/**
 * RR单旋
 * @param {AVLTreeNode<number>} A
 */
function singleRightRotation(A) {
  /* 注意：A必须有一个左子结点B */
  /* 将A与B做左单旋，更新A与B的高度，返回新的根结点B */
  let B = A.right;
  // 注意： 一定要先把B的左子树挂在A的右边
  A.right = B.left;
  // A的右子树的左子树
  B.left = A;
  A.height = Math.max(this.getHeight(A.left), this.getHeight(A.right)) + 1;
  B.height = Math.max(this.getHeight(B.right), this.getHeight(A)) + 1;
  return B;
}

RL 旋转

流程和LR旋转类似，此处不再赘述。

/**
 * 右左旋转
 * @param {AVLTreeNode<number>} A
 * @returns {AVLTreeNode<number>}
 */
function doubleRightLeftRotation(A) {
  /* 注意：A必须有一个右子结点B，且B必须有一个左子结点C */
  /* 将A、B与C做两次单旋，返回新的根结点C */
  /* 将B与C做左单旋，C被返回 */
  A.right = this.singleLeftRotation(A.right);
  /* 将A与C做右单旋，C被返回 */
  return this.singleRightRotation(A);
}

AVL 树的插入

AVL树的插入原理和二叉搜索树的原理类似，只不过每次再插入完成之后，需要进行旋转的调整。

基本流程如下：

首先，如果树空，则插入新结点，更新树高，并且返回；

若树不为空，判断插入值和当前根节点的值的大小，若比当前根节点的值大，则沿着左子树递归，否则，沿着右子树递归（本文不考虑二叉树中存在重复值）。

在已经确定好了是在左还是右子树上插入之后，插入完成，此时，因为我们的插入操作影响到了树高，可能需要进行旋转调整，若左右子树高度绝对值等于 2（我才懒得去记谁减去谁呢），说明当前树已经不再是AVL树了，需要调整。

如果我们是插在当前根节点的左子树上的，那么，肯定是左旋，至于是LL旋转还是LR旋转呢，这就要取决于我们是插入在左子树的左边还是右边的，因此，我们可以通过val < treeNode.left.val知道是插入在左边还是右边。如果这个条件成立，说明是插入在左子树的左边，则执行LL旋转，否则执行LR旋转。

掌握左子树的插入之后，在右子树上的操作就变得简单了，此处不再赘述。

/**
 * 插入子节点
 * @param {number} val
 */
function insert(val) {
  this.root = this._insert(this.root, val);
}

/**
 * 插入子节点
 * @param {AVLTreeNode<number>} treeNode
 * @param {number} val
 * @returns {AVLTreeNode<number>}
 */
function _insert(treeNode, val) {
  /* 将X插入AVL树treeNode中，并且返回调整后的AVL树 */
  if (!treeNode) {
    /* 若插入空树，则新建包含一个结点的树 */
    treeNode = {
      val: val,
      height: 0,
      left: null,
      right: null,
    };
  } else if (val < treeNode.val) {
    /* 插入treeNode的左子树 */
    treeNode.left = this._insert(treeNode.left, val);
    /* 如果需要旋旋 */
    if (this.getHeight(treeNode.left) - this.getHeight(treeNode.right) === 2) {
      if (val < treeNode.left.val) {
        /* 左单旋 */
        treeNode = this.singleLeftRotation(treeNode);
      } else {
        /* 左-右双旋 */
        treeNode = this.doubleLeftRightRotation(treeNode);
      }
    }
  } else if (val > treeNode.val) {
    /* 插入treeNode的右子树 */
    treeNode.right = this._insert(treeNode.right, val);
    /* 如果需要右旋 */
    if (this.getHeight(treeNode.left) - this.getHeight(treeNode.right) === -2) {
      if (val > treeNode.right.val) {
        /* 右单旋 */
        treeNode = this.singleRightRotation(treeNode);
      } else {
        /* 右-左双旋 */
        treeNode = this.doubleRightLeftRotation(treeNode);
      }
    }
  }
  /* 更新树高 */
  treeNode.height =
    Math.max(this.getHeight(treeNode.left), this.getHeight(treeNode.right)) + 1;
  return treeNode;
}

AVL 树的删除

AVL树的删除操作，是插入操作的逆过程，我们以递归实现为思路，首先删除操作必须是基于一个二叉搜索树的删除， 如果当前是空树，则无法删除，如果当前根节点的值比待删除值大，则沿着左子树递归删除，反之则沿着右子树递归删除；如果当前根节点的值待删除值相同，则说明这个节点就是要删除的值，此时，就要看当前节点是一个什么样的情况了，如果它同时具有左右儿子，那么，我们可以从它的右子树里面找一个最小值（左子树里面找一个最大值也可以），然后把找到的最值节点拷贝到当前这个位置上，并且从当前节点的子树开始，递归的去删除它的最值（如果你之前是用的是右子树的最小值，就从右子树出发删除最小值，使用左子树的最大值同理），最后我们的问题始终转换为删除不同时具有左右子节点的问题。如果当前节点没有左右儿子，直接把treeNode指针标记为空即可，如果当前节点只有左儿子，那么直接用当前节点的左儿子指针覆盖treeNode指针即可，如果当前节点只有右儿子，那么直接用当前节点的右儿子指针覆盖treeNode指针即可，

因为我们删除了树的节点，影响到了高度，所以现在需要根据树高进行旋转调整。

比如现在你删除了右子树上面的节点，若是影响了树的高度的话（左右子树高度差大于等于 2），我们即需要进行左旋转，至于是LL旋转还是LR旋转，得取决于当前左子树的左右子树的高度，如果左子树的左子树树高大于等于左子树的右子树树高，说明左边高，则进行LL旋转，否则LR旋转。（分不清这儿的同学可以看一下上文旋转操作的图示）。

下图表示的是删除A的右子节点之后，其中B的左子树树高大于等于B的左子树的树高（取得等于的时候是B的右子树存在时），这种情况下进行的是LL旋转。

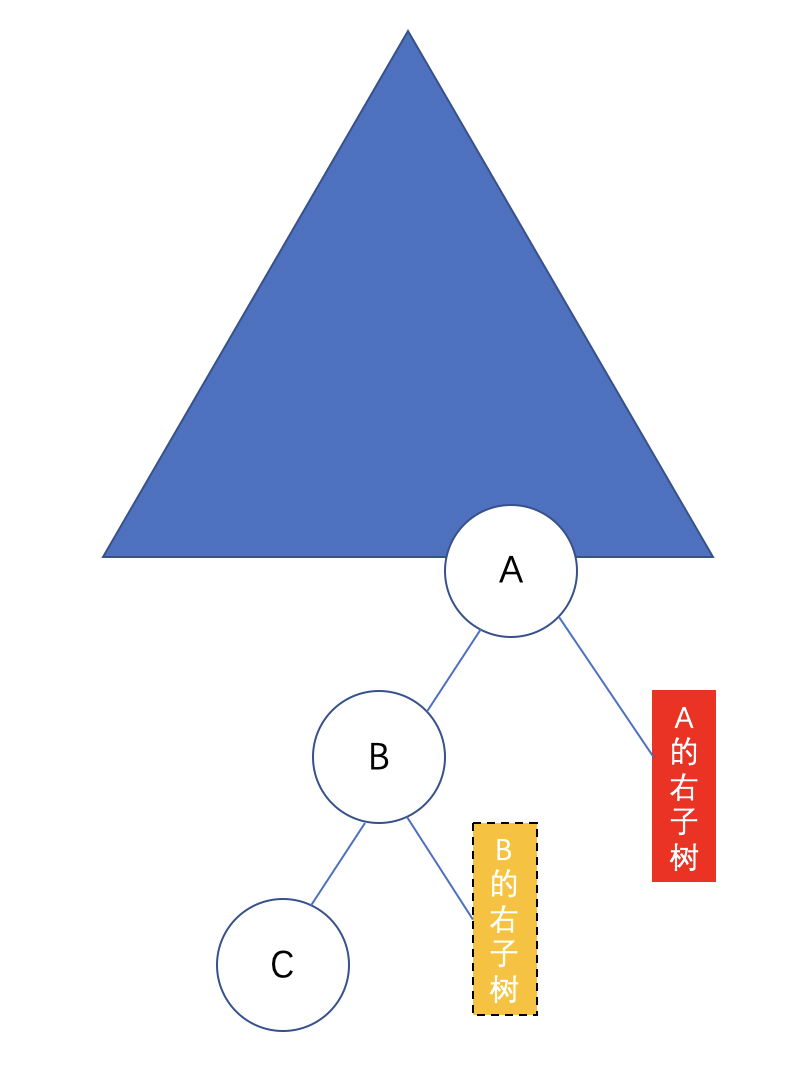
下图表示的是删除A的右子节点之后，其中B的右子树树高，大于B的左子树的树高，这种情况下进行的是LR旋转。

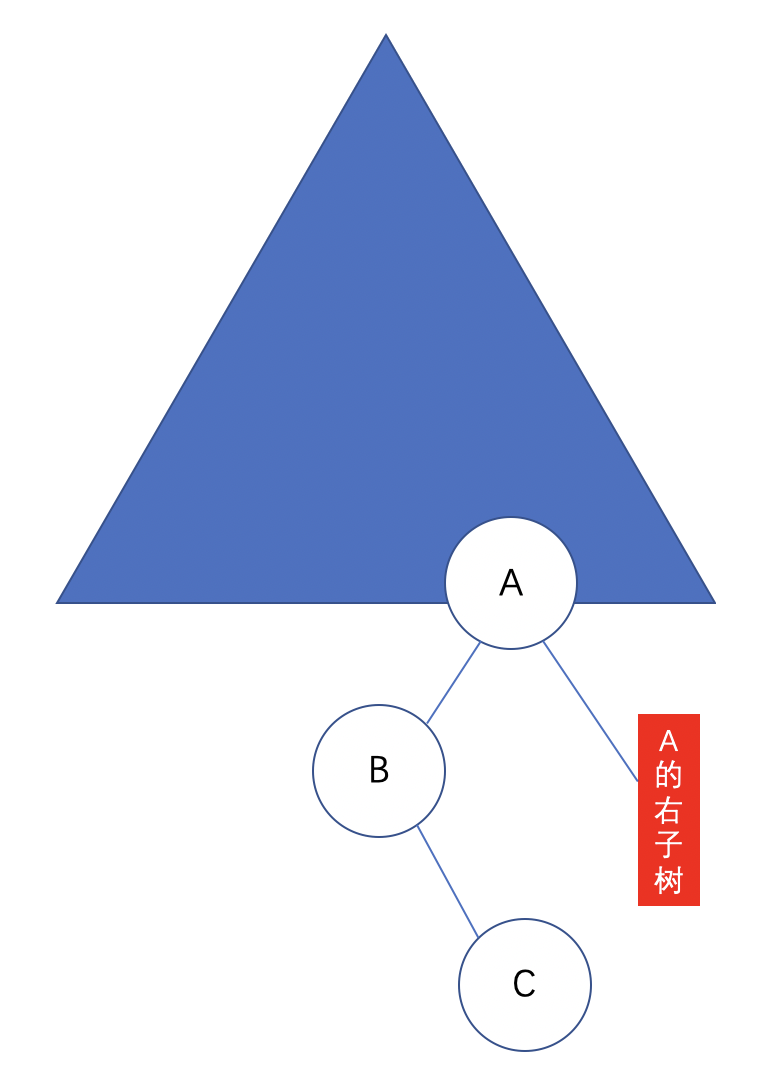
当删除节点是某个节点的左叶子节点的情况时上面两种情况差不多，就不再赘述。

当这些操作都进行完毕之后，千万别忘了更新树高。

一次删除，可能需要多次回溯才可能最终使树变得平衡，因为我们使用的是递归算法，当递归调用退栈的时候，将会根据左右子树的高度决定是否进行旋转调整。

/**
 * 在AVL树中查找最小值
 * @param {AVLTreeNode<number>} treeNode
 * @returns
 */
function findMin(treeNode) {
  let minTreeNode = null;
  while (treeNode) {
    minTreeNode = treeNode;
    treeNode = treeNode.left;
  }
  return minTreeNode;
}

/**
 * 删除子节点
 * @param {number} val
 */
function delete(val) {
  this.root = this._delete(this.root, val);
}

/**
 * 辅助函数：删除子节点
 * @param {AVLTreeNode<number>} treeNode
 * @param {number} delVal
 * @returns
 */
function _delete(treeNode, delVal) {
  if (treeNode === null) {
    // 空树，无法删除
    return null;
  } else if (delVal < treeNode.val) {
    // val 位于左子树，其实就是相当于右子树的插入，所以在调整的时候，执行右旋
    treeNode.left = this._delete(treeNode.left, delVal);
    // 更新树高
    treeNode.height =
      Math.max(
        this.getHeight(treeNode.left),
        this.getHeight(treeNode.right)
      ) + 1;
    if (
      Math.abs(
        this.getHeight(treeNode.right) - this.getHeight(treeNode.left)
      ) === 2
    ) {
      // 在回溯时，仍然有可能有调整子树的需求
      if (
        this.getHeight(treeNode.right.right) >=
        this.getHeight(treeNode.right.left)
      ) {
        treeNode = this.singleRightRotation(treeNode);
      } else {
        treeNode = this.doubleLeftRightRotation(treeNode);
      }
    }
  } else if (delVal > treeNode.val) {
    // val 位于右子树删除，其实就是相当于是左子树插入
    treeNode.right = this._delete(treeNode.right, delVal);
    // 更新树高
    treeNode.height =
      Math.max(
        this.getHeight(treeNode.left),
        this.getHeight(treeNode.right)
      ) + 1;
    if (
      Math.abs(
        this.getHeight(treeNode.left) - this.getHeight(treeNode.right)
      ) === 2
    ) {
      // 在回溯时，仍然有可能有调整子树的需求
      if (
        this.getHeight(treeNode.left.left) >=
        this.getHeight(treeNode.left.right)
      ) {
        treeNode = this.singleLeftRotation(treeNode);
      } else {
        treeNode = this.doubleLeftRightRotation(treeNode);
      }
    }
  } else if (treeNode.left && treeNode.right) {
    /* 如果待删除节点同时存在左右儿子节点 */
    // 找到右子树的最小节点
    let rightSubTreeMinNode = this.findMin(treeNode.right);
    // 用右子树上的最小节点替换当前值，然后再从当前右子树触发，递归的删除右子树上的最小值。
    treeNode.val = rightSubTreeMinNode.val;
    treeNode.right = this._delete(treeNode.right, treeNode.val);
  } else {
    /* 如果待删除节点只有左儿子节点，那么把它的左儿子直接赋值给它自己，相当于移除了待删除节点 */
    if (treeNode.right === null) {
      treeNode = treeNode.left;
    } else if (treeNode.left === null) {
      /* 如果待删除节点只有右儿子节点，那么把它的右儿子直接赋值给它自己，相当于移除了待删除节点 */
      treeNode = treeNode.right;
    } else {
      /* 如果待删除节点没有左右儿子节点，直接赋值为空，相当于移除了待删除节点 */
      treeNode = null;
    }
  }
  return treeNode;
}

复杂度分析

AVL树的完整代码如下：

/**
 * 平衡二叉树的实现
 */
class AVLTree {
  /**
   * 根节点
   * @type {AVLTreeNode<number> | null}
   */
  root = null;

  /**
   * 获取以treeNode为根节点的树高
   * @param {AVLTreeNode<number>} treeNode
   */
  getHeight(treeNode) {
    return treeNode ? treeNode.height : 0;
  }

  /**
   * 左单旋
   * @param {AVLTreeNode<number>} A
   * @returns {AVLTreeNode<number>}
   */
  singleLeftRotation(A) {
    /* 注意：A必须有一个左子结点B */
    /* 将A与B做左单旋，更新A与B的高度，返回新的根结点B */
    // 当前树节点的左子树
    let B = A.left;
    // 注意： 一定要先把B的右子树挂在A的左边
    A.left = B.right;
    B.right = A;
    A.height = Math.max(this.getHeight(A.left), this.getHeight(A.right)) + 1;
    B.height = Math.max(this.getHeight(B.left), this.getHeight(A)) + 1;
    return B;
  }

  /**
   * 右单旋
   * @param {AVLTreeNode<number>} A
   */
  singleRightRotation(A) {
    /* 注意：A必须有一个左子结点B */
    /* 将A与B做左单旋，更新A与B的高度，返回新的根结点B */
    let B = A.right;
    // 注意： 一定要先把B的左子树挂在A的右边
    A.right = B.left;
    // A的右子树的左子树
    B.left = A;
    A.height = Math.max(this.getHeight(A.left), this.getHeight(A.right)) + 1;
    B.height = Math.max(this.getHeight(B.right), this.getHeight(A)) + 1;
    return B;
  }

  /**
   * 左右旋转
   * @param {AVLTreeNode<number>} A
   * @returns {AVLTreeNode<number>}
   */
  doubleLeftRightRotation(A) {
    /* 注意：A必须有一个左子结点B，且B必须有一个右子结点C */
    /* 将A、B与C做两次单旋，返回新的根结点C */
    /* 将B与C做右单旋，C被返回 */
    A.left = this.singleRightRotation(A.left);
    /* 将A与C做左单旋，C被返回 */
    return this.singleLeftRotation(A);
  }

  /**
   * 右左旋转
   * @param {AVLTreeNode<number>} A
   * @returns {AVLTreeNode<number>}
   */
  doubleRightLeftRotation(A) {
    /* 注意：A必须有一个右子结点B，且B必须有一个左子结点C */
    /* 将A、B与C做两次单旋，返回新的根结点C */
    /* 将B与C做左单旋，C被返回 */
    A.right = this.singleLeftRotation(A.right);
    /* 将A与C做右单旋，C被返回 */
    return this.singleRightRotation(A);
  }

  /**
   * 查找指定值是否在二叉搜索树中存在
   * @param {number} val
   * @returns {AVLTreeNode<number>}
   */
  find(val) {
    return this._find(val, this.root);
  }

  /**
   * 查找辅助函数
   * @param {number} val
   * @param {AVLTreeNode<number>} treeNode
   */
  _find(val, treeNode) {
    let node = treeNode;
    while (node) {
      if (node.val == val) {
        break;
      } else if (node.val > val) {
        // 沿着左子树查找
        node = node.left;
      } else if (node.val < val) {
        // 沿着右子树查找
        node = node.right;
      }
    }
    return node;
  }

  /**
   * 在AVL树中查找最小值
   * @param {AVLTreeNode<number>} treeNode
   * @returns
   */
  findMin(treeNode) {
    let minTreeNode = null;
    while (treeNode) {
      minTreeNode = treeNode;
      treeNode = treeNode.left;
    }
    return minTreeNode;
  }

  /**
   * 插入子节点
   * @param {number} val
   */
  insert(val) {
    this.root = this._insert(this.root, val);
  }

  /**
   * 删除子节点
   * @param {number} val
   */
  delete(val) {
    this.root = this._delete(this.root, val);
  }

  /**
   * 辅助函数：删除子节点
   * @param {AVLTreeNode<number>} treeNode
   * @param {number} delVal
   * @returns
   */
  _delete(treeNode, delVal) {
    if (treeNode === null) {
      // 空树，无法删除
      return null;
    } else if (delVal < treeNode.val) {
      // val 位于左子树，其实就是相当于右子树的插入，所以在调整的时候，执行右旋
      treeNode.left = this._delete(treeNode.left, delVal);
      // 更新树高
      treeNode.height =
        Math.max(
          this.getHeight(treeNode.left),
          this.getHeight(treeNode.right)
        ) + 1;
      if (
        Math.abs(
          this.getHeight(treeNode.right) - this.getHeight(treeNode.left)
        ) === 2
      ) {
        if (
          this.getHeight(treeNode.right.right) >=
          this.getHeight(treeNode.right.left)
        ) {
          treeNode = this.singleRightRotation(treeNode);
        } else {
          treeNode = this.doubleLeftRightRotation(treeNode);
        }
      }
    } else if (delVal > treeNode.val) {
      // val 位于右子树删除，其实就是相当于是左子树插入
      treeNode.right = this._delete(treeNode.right, delVal);
      // 更新树高
      treeNode.height =
        Math.max(
          this.getHeight(treeNode.left),
          this.getHeight(treeNode.right)
        ) + 1;
      if (
        Math.abs(
          this.getHeight(treeNode.left) - this.getHeight(treeNode.right)
        ) === 2
      ) {
        if (
          this.getHeight(treeNode.left.left) >=
          this.getHeight(treeNode.left.right)
        ) {
          treeNode = this.singleLeftRotation(treeNode);
        } else {
          treeNode = this.doubleLeftRightRotation(treeNode);
        }
      }
    } else if (treeNode.left && treeNode.right) {
      /* 如果待删除节点同时存在左右儿子节点 */
      // 找到右子树的最小节点
      let rightSubTreeMinNode = this.findMin(treeNode.right);
      // 用右子树上的最小节点替换当前值，然后再从当前右子树触发，递归的删除右子树上的最小值。
      treeNode.val = rightSubTreeMinNode.val;
      treeNode.right = this._delete(treeNode.right, treeNode.val);
    } else {
      /* 如果待删除节点只有左儿子节点，那么把它的左儿子直接赋值给它自己，相当于移除了待删除节点 */
      if (treeNode.right === null) {
        treeNode = treeNode.left;
      } else if (treeNode.left === null) {
        /* 如果待删除节点只有右儿子节点，那么把它的右儿子直接赋值给它自己，相当于移除了待删除节点 */
        treeNode = treeNode.right;
      } else {
        /* 如果待删除节点没有左右儿子节点，直接赋值为空，相当于移除了待删除节点 */
        treeNode = null;
      }
    }
    return treeNode;
  }

  /**
   * 辅助函数：插入子节点
   * @param {AVLTreeNode<number>} treeNode
   * @param {number} val
   * @returns {AVLTreeNode<number>}
   */
  _insert(treeNode, val) {
    /* 将X插入AVL树treeNode中，并且返回调整后的AVL树 */
    if (!treeNode) {
      /* 若插入空树，则新建包含一个结点的树 */
      treeNode = {
        val: val,
        height: 0,
        left: null,
        right: null,
      };
    } else if (val < treeNode.val) {
      /* 插入treeNode的左子树 */
      treeNode.left = this._insert(treeNode.left, val);
      /* 如果需要左旋 */
      if (
        Math.abs(
          this.getHeight(treeNode.left) - this.getHeight(treeNode.right)
        ) === 2
      ) {
        if (val < treeNode.left.val) {
          /* 左单旋 */
          treeNode = this.singleLeftRotation(treeNode);
        } else {
          /* 左-右双旋 */
          treeNode = this.doubleLeftRightRotation(treeNode);
        }
      }
    } else if (val > treeNode.val) {
      /* 插入treeNode的右子树 */
      treeNode.right = this._insert(treeNode.right, val);
      /* 如果需要右旋 */
      if (
        Math.abs(
          this.getHeight(treeNode.left) - this.getHeight(treeNode.right)
        ) === 2
      ) {
        if (val > treeNode.right.val) {
          /* 右单旋 */
          treeNode = this.singleRightRotation(treeNode);
        } else {
          /* 右-左双旋 */
          treeNode = this.doubleRightLeftRotation(treeNode);
        }
      }
    }
    /* 更新树高 */
    treeNode.height =
      Math.max(this.getHeight(treeNode.left), this.getHeight(treeNode.right)) +
      1;
    return treeNode;
  }
}

AVL树的插入和删除时间复杂度都是O(log n)，具体的分析过程，有兴趣的同学请参考相应的论文资料。