跳表(跳跃链表)

在前文，我们有介绍链表，链表的插入和删除是较为高效的，因为只需要修改前驱和后继指针，但是链表无法做到像数组那样的随机化访问，每次查找的平均算法复杂度为O(N)，这是链表的一个比较大的缺点。

跳跃链表，简称跳表，在原有的有序链表上面增加了多级索引，通过索引来实现快速查找，是一个随机化的数据结构，实质就是一种可以进行二分查找的有序链表，是在 O(log*n)时间内完成增加、删除、搜索操作的数据结构。

跳表相比于堆与AVL树(或红黑树)，其功能与性能相当，但跳表的代码长度相较下更短，其设计思想与链表相似。

跳表不仅能提高搜索性能，同时也可以提高插入和删除操作的性能。

最底层是原始的链表，接着根据生成的随机数决定是否继续向上生成当前节点的后继节点，直到把它的最大层都填满(以 4 层举例)，大致如下图：

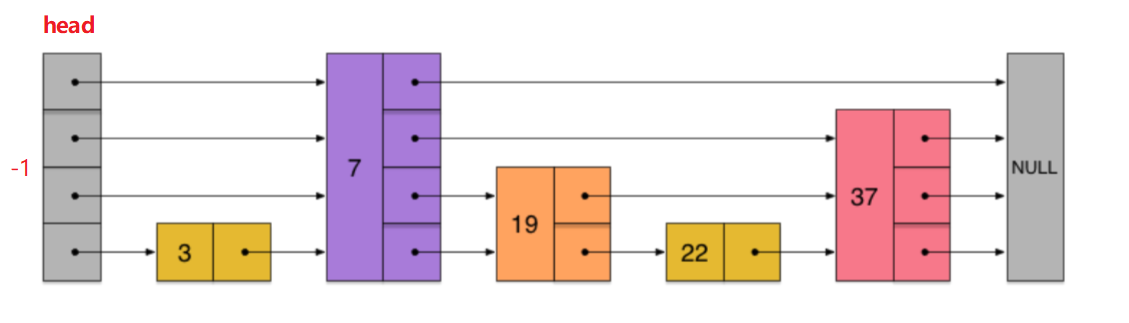
第一个节点是哨兵节点，跳表的节点就像鳞次栉比的山峰，不同的山峰之间的相同层上就是建立的引用关系，用来加快查找的速度。

需要注意的是，比如对于图中的节点3，并不是说它的next指针数组的长度为 1，而依然是 4 层，只不过，除了最底层的内容以外，其余都存的是null，我们在查找时，某层就会忽略这个节点，这样就实现了跳跃。

因此，可以采用如下方式来表示跳表中的节点：

class ListNode {
  /**
   * @type {number}
   */
  val = -1;
  /**
   * @type {ListNode[]}
   */
  next = [];
  /**
   * @param {number} val
   * @param {number} level
   */
  constructor(val, level) {
    this.val = val;
    // 初始化指定高度的数组
    this.next = Array.from({
      length: level,
    }).fill(null);
  }
}

查找辅助函数

因为跳表是基于二分查找的，在查找的过程中，我们总是从最上层查找到最下层的，我们需要把每次的位置记下来，这样不管是查找， 插入，删除都可以很方便的使用这个路径。

这节我们先不详细阐述辅助函数，同学们可以看完插入节之后再回头来看这节的内容。

/**
 * 查找辅助函数，记录从上至下查找路径
 * @param {number} target
 */
function find(target) {
  let path = Array.from({
    length: this.level,
  }).fill(null);
  // 从头节点开始遍历每一层，p最开始就是头结点
  let p = this.head;
  for (let i = this.level - 1; i >= 0; i--) {
    // 从上层往下层找
    while (p.next[i] && p.next[i].val < target) {
      // 如果当前层 i 的 next 不为空，且它的值小于 target，则 p 往后走指向这一层 p 的 next，下层的p就从这一层的p开始
      p = p.next[i];
    }
    // 退出 while 时说明找到了第 i 层小于 target 的最大节点就是 p
    path[i] = p;
  }
  return path;
}

查找

上面的查找辅助函数我们并没有给出运行过程，因为需要结合着一个操作来解释它才更好描述。

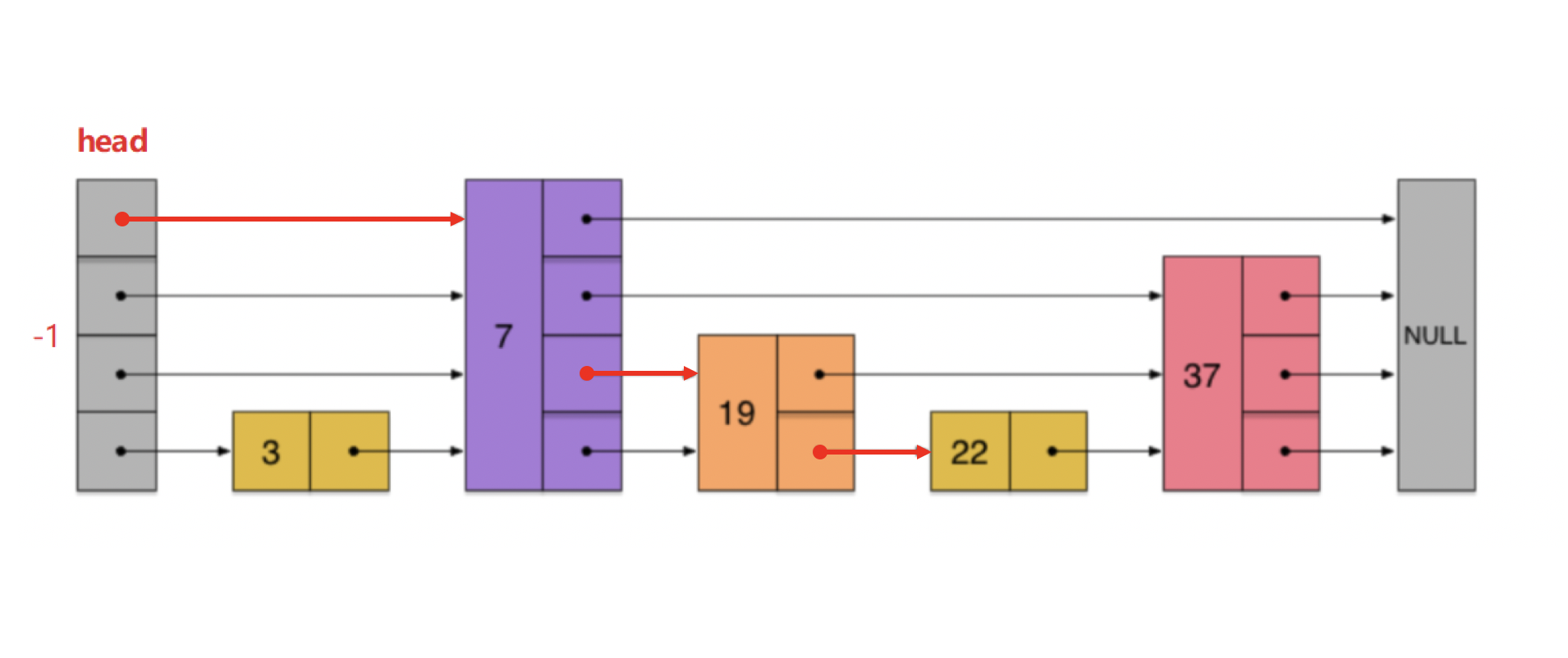
比如，现在跳表的存储如上图所示，查找一个存在的情况，假设要查找22。

首先，从head的最顶层开始查找，向后找到节点7，接着找，发现已经到末尾，因此，路径的第一层节点可以确定为节点7。

接着，从head的第二层开始查找，这次，我们要直接从节点7开始向后找，发现下一节点为37，但是37大于22，因此，路径的第 2 层的节点可以确定为节点7。

然后，从head的第三层开始查找，这次，我们要直接从节点7开始向后找，发现下一节点为19，接着往后找，发现下一节点是37，但是37大于22，因此，路径的第 3 层的节点可以确定为节点19。

最后，从head的最后一层开始查找，这次，我们要直接从19开始向后找，发现下一节点为22，但是22等于22，因此，路径的第 4 层的节点可以确定为节点19。

有同学可能会问，为什么19后面就一定是22呢？，因为这个跳表里面的节点太少，不太好理解，假设有很多节点，比如19后面有20，21，循环是要遇到大于等于22的才会停止的。

比如，现在跳表的存储如表示方法节所描述所示，查找一个不存在的情况，假设要查找23。

首先，从head的最顶层开始查找，向后找到7，接着找，发现已经到末尾，因此，路径的第一层节点可以确定为节点7。

接着，从head的第二层开始查找，这次，我们要直接从7开始向后找，发现下一节点为37，但是37大于22，因此，路径的第 2 层的节点可以确定为节点7。

然后，从head的第三层开始查找，这次，我们要直接从7开始向后找，发现下一节点为19，接着往后找，发现下一节点是37，但是37大于22，因此，路径的第 3 层的节点可以确定为节点19。

最后，从head的最后一层开始查找，这次，我们要直接从19开始向后找，发现下一节点为22，但是22小于23，接着向后查找，发现下一节点是37，37大于23，因此，路径的第 4 层的节点可以确定为节点22。

因为节点22的下一节点是33，因此可以得知，23在表中不存在。

上述的查找过程，大致如下图所示：

/**
 * 查找元素
 * @param {number} target
 * @returns
 */
function search(target) {
  // 先找到每一层 i 小于目标值 target 的最大节点 path[i]
  let path = this.find(target);
  // 因为最下层【0】的节点是全的，所以只需要判断 target 是否在第 0 层即可，而 path[0] 正好就是小于 target 的最大节点，如果 path[0]->next[0] 的值不是 target 说明没有这个元素
  let p = path[0].next[0];
  return p != null && p.val == target;
}

在明白查找过程之后，大家再回过头来看我们的find函数就一目了然了。如果你掌握了跳表的查找，那么恭喜你，整个跳表的知识点你已经掌握了 80%了。

插入

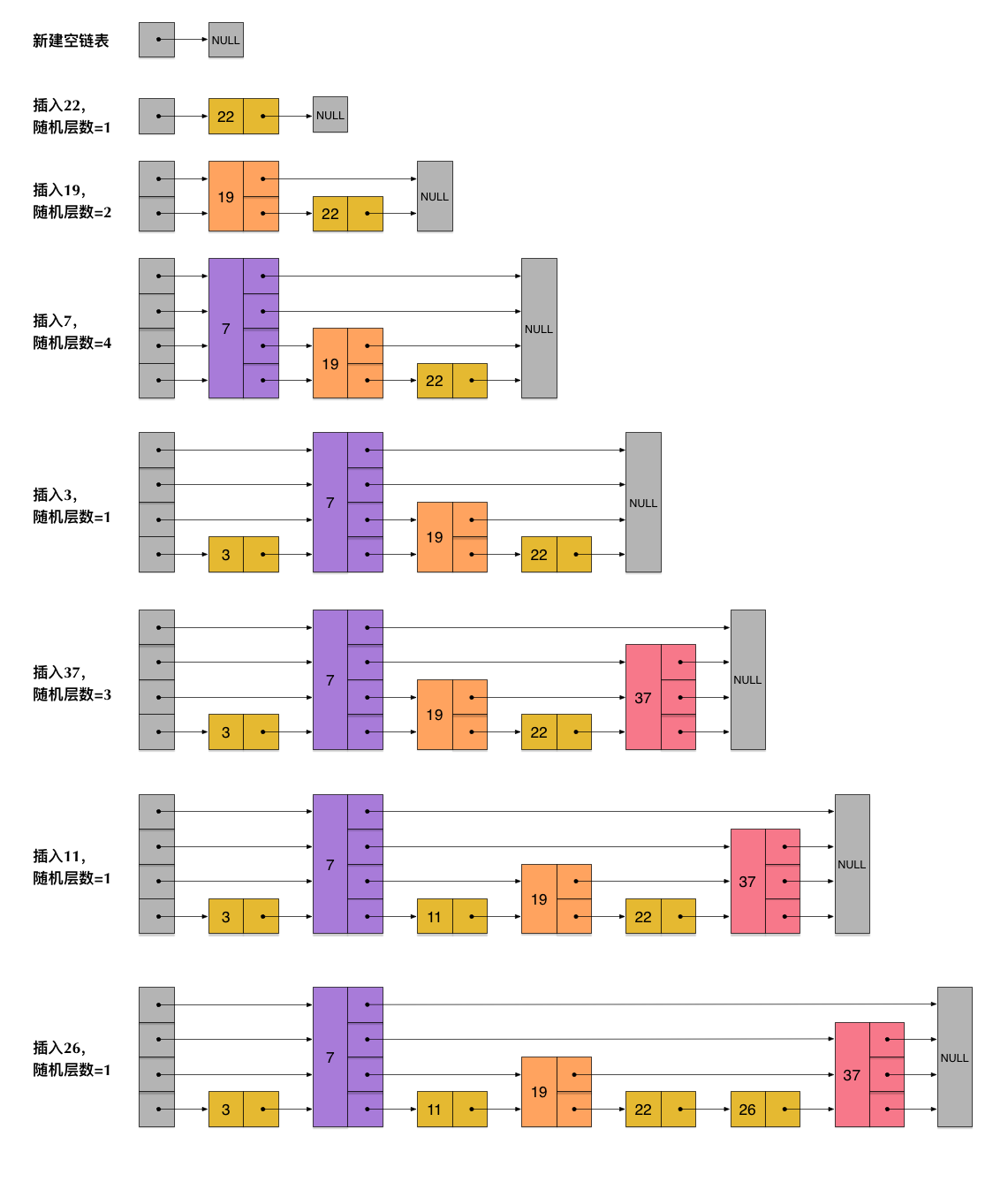
对于插入操作，我们需要根据随机数据来决定当前节点的高度。下文以0.5为分界线，若超过的话，我们就不断的建立后继指针，否则就在某层提前结束。这是一个跟单链表类似的操作。

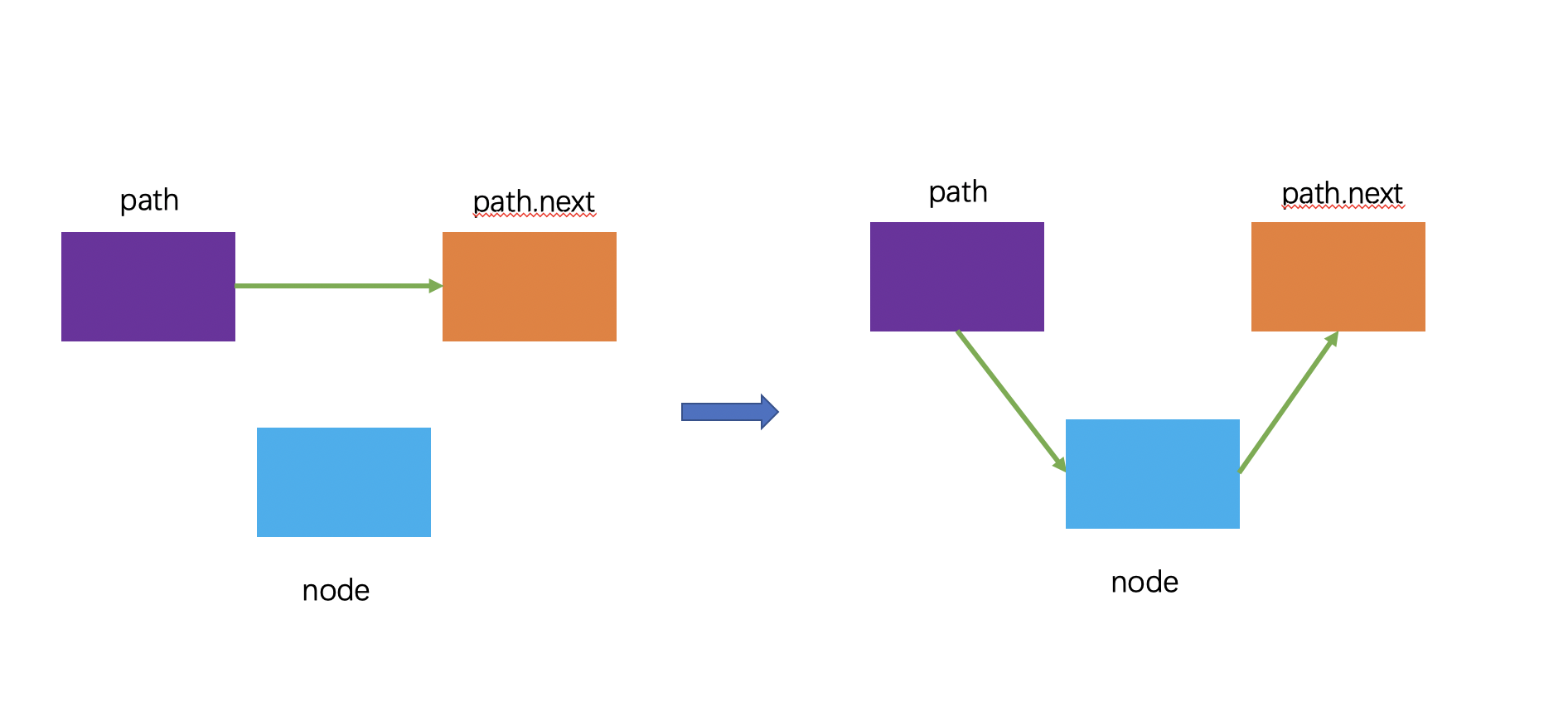
首先，find辅助函数已经找到了每层的节点，那么对于每层的节点，即path[i]，我们可以直接将新创建的节点加入到链表中。

即：

// 创建一个新的节点
let node = new ListNode(num, this.level);
// 将对应层的next指针指向path的next指针的对应层
node.next[i] = path[i].next[i];
// 将path的next指针指向node
path[i].next[i] = node;
/**
 * node.next = path.next
 * path.next = node
 */

如果看着比较迷糊的同学，你可以先不考虑i这个变量对插入操作的影响，先将其抽象为普通的链表插入来理解，如代码中的注释所示，抽象流程如下：

随机数即控制了我们要建立多少层的关联，因此整个插入流程如下图所示：

/**
 * 插入元素
 * @param {number} num
 */
function add(num) {
  // 先找到每一层 i 小于目标值 target 的最大节点 path[i]
  let path = this.find(num);
  // 创建要插入的新节点
  let node = new ListNode(num, this.level);
  for (let i = 0; i < this.level; i++) {
    // 遍历每一层，从下往上插入新节点
    // 这两步就是单链表的插入
    node.next[i] = path[i].next[i];
    path[i].next[i] = node;
    // 每一层有 50% 的概率不插入新节点
    if (Math.random() > 0.5) {
      break;
    }
  }
}

删除

删除操作也相对比较简单，首先，我们需要确定待删除的值在跳表中是否存在，为什么我们不直接调用查找函数而是要调用辅助函数呢，这是因为我们需要知道待删除节点的前驱节点。

比如，现在要删除节点22，经过前置查找，我们能确定下来节点22的前置指针，接着，就可以直接对每层的指针进行删除。

需要注意的是，待删除节点可能不是每层都有的，我们在删除的时候，必须从底层删至上层，发现当前层为空的话，就可提前结束循环了。

/**
 * 删除元素
 * @param {number} num
 * @returns
 */
function remove(num) {
  // 先找到每一层 i 小于目标值 target 的最大节点 path[i]
  let path = this.find(num);
  // 先判断 num 是否存在，不存在直接返回 false
  // 第 0 层存储的是全部节点，所以只需要判断 path[0]->next[0]（第 0 层小于 num 的最大节点的在第 0 层的 next） 是不是 num 即可
  let p = path[0].next[0];
  if (!p || p.val != num) {
    console.warn("要删除的值不存在!");
    return false;
  }
  // 否则删除每一层的 num，如果 path[i]->next[i] == p 说明第 i 层存在 p
  for (let i = 0; i < this.level && path[i].next[i] === p; i++) {
    // 单链表删除
    path[i].next[i] = p.next[i];
  }
  p = null; // 删除节点 p，防止内存泄漏
  return true;
}

结语

跳表也是典型的空间换时间的应用场景，在大名鼎鼎的Redis中，就使用了跳表。

时间复杂度

跳表的查询、删除、插入的时间复杂度近似O(log*n)，其证明过程非常复杂，具体的分析过程超出了本文的讨论范畴，有兴趣的同学可以参考原始论文 (opens new window)。

空间复杂度

O(level*n)，和层数以及节点数相关，每个节点最大的开销就是存储在每一层的next。

跳表的完整实现如下：

class ListNode {
  /**
   * @type {number}
   */
  val = -1;
  /**
   * @type {ListNode[]}
   */
  next = [];
  /**
   * @param {number} val
   * @param {number} level
   */
  constructor(val, level) {
    this.val = val;
    // 初始化指定高度的数组
    this.next = Array.from({
      length: level,
    }).fill(null);
  }
}

class SkipList {
  /**
   * 最大层数
   * @type {number}
   */
  level = 8;
  /**
   * 头结点
   * @type {ListNode | null}
   */
  head = null;

  constructor() {
    this.head = new ListNode(-1, this.level);
  }
  /**
   * 查找辅助函数，记录从上至下查找路径
   * @param {number} target
   */
  find(target) {
    let path = Array.from({
      length: this.level,
    }).fill(null);
    // 从头节点开始遍历每一层
    let p = this.head;
    for (let i = this.level - 1; i >= 0; i--) {
      // 从上层往下层找
      while (p.next[i] && p.next[i].val < target) {
        // 如果当前层 i 的 next 不为空，且它的值小于 target，则 p 往后走指向这一层 p 的 next
        p = p.next[i];
      }
      // 退出 while 时说明找到了第 i 层小于 target 的最大节点就是 p
      path[i] = p;
    }
    return path;
  }
  /**
   * 查找元素
   * @param {number} target
   * @returns
   */
  search(target) {
    // 先找到每一层 i 小于目标值 target 的最大节点 path[i]
    let path = this.find(target);
    // 因为最下层【0】的节点是全的，所以只需要判断 target 是否在第 0 层即可，而 path[0] 正好就是小于 target 的最大节点，如果 path[0]->next[0] 的值不是 target 说明没有这个元素
    let p = path[0].next[0];
    return p != null && p.val == target;
  }

  /**
   * 插入元素
   * @param {number} num
   */
  add(num) {
    // 先找到每一层 i 小于目标值 target 的最大节点 path[i]
    let path = this.find(num);
    // 创建要插入的新节点
    let node = new ListNode(num, this.level);
    for (let i = 0; i < this.level; i++) {
      // 遍历每一层，从下往上插入新节点
      // 这两步就是单链表的插入
      node.next[i] = path[i].next[i];
      path[i].next[i] = node;
      // 每一层有 50% 的概率不插入新节点
      if (Math.random() > 0.5) {
        break;
      }
    }
  }
  /**
   * 删除元素
   * @param {number} num
   * @returns
   */
  remove(num) {
    // 先找到每一层 i 小于目标值 target 的最大节点 path[i]
    let path = this.find(num);
    // 先判断 num 是否存在，不存在直接返回 false
    // 第 0 层存储的是全部节点，所以只需要判断 path[0]->next[0]（第 0 层小于 num 的最大节点的在第 0 层的 next） 是不是 num 即可
    let p = path[0].next[0];
    if (!p || p.val != num) {
      console.warn("要删除的值不存在!");
      return false;
    }
    // 否则删除每一层的 num，如果 path[i]->next[i] == p 说明第 i 层存在 p
    for (let i = 0; i < this.level && path[i].next[i] == p; i++) {
      // 单链表删除
      path[i].next[i] = p.next[i];
    }
    // 删除节点 p，防止内存泄漏
    p = null;
    return true;
  }
}