# KMP 算法
KMP 算法是什么?主要解决的问题是在给定一个字符串 template,快速的发现是否在 template 存在子串 pattern。
KMP 算法是一种改进的字符串匹配算法,由D.E.Knuth,J.H.Morris 和 V.R.Pratt 提出的,所以由 3 位杰出的前辈的名字各取了一个字母得名。在某些版本的《数据结构》这门课中,存在于“串”这一章节。
KMP 算法是出了名的难,其思想可能大多数同学都能掌握,但关键是求next数组,很多同学都没有理解为什么简短的几行代码就可实现神奇的效果,网上的博客或视频大多对于next数组对求解过程也是一笔带过,而KMP算法如果你不搞懂对next数组求解过程,那么你就不算真正懂得的 KMP 算法。
# 朴素法
在介绍 KMP 算法之前不得不提蛮力匹配算法,因为了解了蛮力匹配算法才能通过比较知道 KMP 算法的优势。
之所以说它是蛮力匹配算法,设定 2 个指针,指针表示在主串上移动的位置,j 指针表示在目标字符串上的位置,就是通过一位一位的去比较,如果匹配失败,则 j 指针归 0,i 指针向后挪动一位,这其实并没有把之前子串上已经匹配到的内容利用起来,所以这个算法是快不起来的。
function subString(tpl, pattern) {
let m = tpl.length;
let n = pattern.length;
for (let i = 0; i < m - n; ++i) {
let j = 0;
while (j < n && tpl[i + j] == pattern[j]) {
++j;
}
if (j == n) {
return i;
}
}
return -1;
}
其大概得算法流程如下:
# 朴素法的复杂度分析
朴素法是简单的两个循环相叠加,因此其时间复杂度是O(m*n),m 和 n 分别为两个字符串的长度
# KMP
KMP 算法的聪明之处就是可以把之前已经匹配过的信息利用起来,用最小的代价知道我们下一次应该从哪个位置开始匹配。
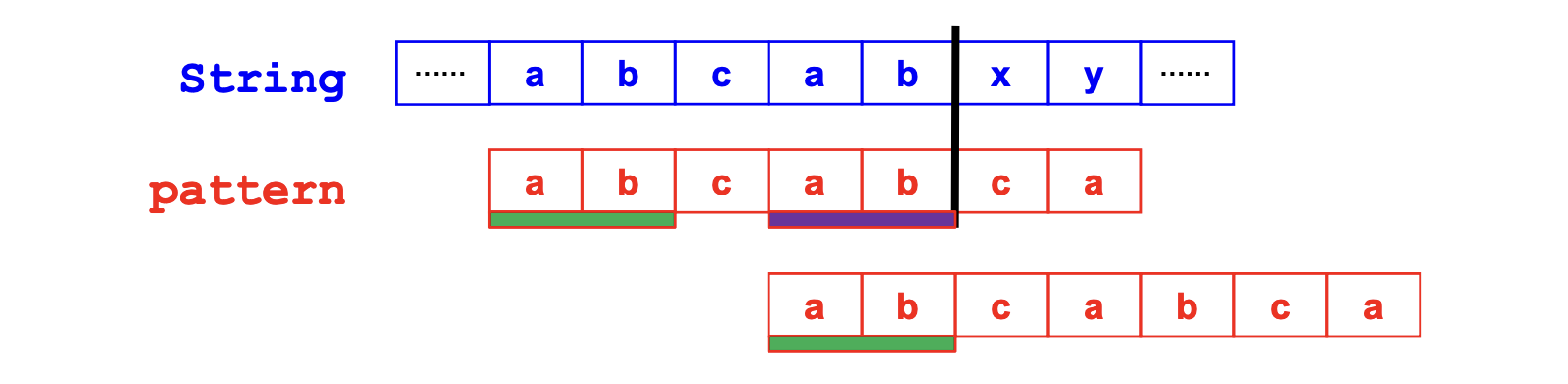
假设现在在 x 和 c 的位置发生失配,那么,我们只需要把模式串pattern向前进 c 之前的最长前后公共子串的长度,即图上的 ab 子串。
因为只有前后公共子串的话,你挪动过去才有可能相配啊。简单一点儿的例子就好比一把两头都可以拧螺丝的扳手,你把这头拿去拧螺丝,跟把另外一头拿去拧螺丝,必须得跟螺丝的规格相配,如果都配的话,那么就无所谓你用那一头拧了。
在明白匹配失败之后的操作之后,我们就需要去计算这个最长前后公共子串,即上文所说的next数组。
为什么我们要先求next数组呢,可以看到,我们的pattern字符串其实是给定的,在匹配的过程中是不会发生变化的,那么,在每次失配的时候,我们一定知道当前失配位置前面是什么样的字符串,利用哈希表的思想,我们可以事先把每个位置的最长公共前后缀先算出来。
接下来就是给出 KMP 算法最关键的 next 数组 求解过程:
假设我们有如下pattern: abcabca
对于子串a(即在匹配的时候,在它的下一个位置 b这个位置发生失配,后面也是这个意思,不赘述),没有公共前后缀,所以计为 0。
对于子串ab,前缀有a, 后缀b,没有相同的前后缀,计为 0;
对于子串abc,前缀a,ab; 后缀c,bc,没有相同的前后缀,计为 0;
对于子串abca,前缀有a,ab,abc;后缀有a,ca,bca,最大公共前后缀a,计为 1;
对于子串abcab,前缀有a,ab,abc,abca;后缀有b,ab,cab,bcab,最大公共前后缀ab,计为 2;
对于子串abcabc,前缀有a,ab,abc,abca,abcab;后缀有c,bc,abc,cabc,bcabc,最大公共前后缀abc,计为 3;
其实最后一个我们是没有多大的算的必要的,因为要在最后一个 a 的后面一位发生失配,这个可能吗?都匹配成功了,还需要什么匹配呢,但是只不过我们算next数组的过程中,没有必要去对这个进行特值处理,为了方便编程,所以还是会将其计算在里面。
所以对于子串abcabca,前缀有a,ab,abc,abca,abcab,abcabc;后缀有 a, ca,bca,abca,cabca,bcabca,最大公共前后缀a,计为 1;
列一个表格,如下:
| a | b | c | a | b | c | a |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 2 | 3 | 1 |
刚才我们已经知道最长公共前后缀的求解方法了,接下来开始思考一下怎么用代码去实现。
首先看一下,比较朴素的方法。
首部取一个字符,尾部取一个字符比较,继续重复这个操作,2 个字符进行比较,不断继续重复这个操作,直到 j 个字符串的长度。
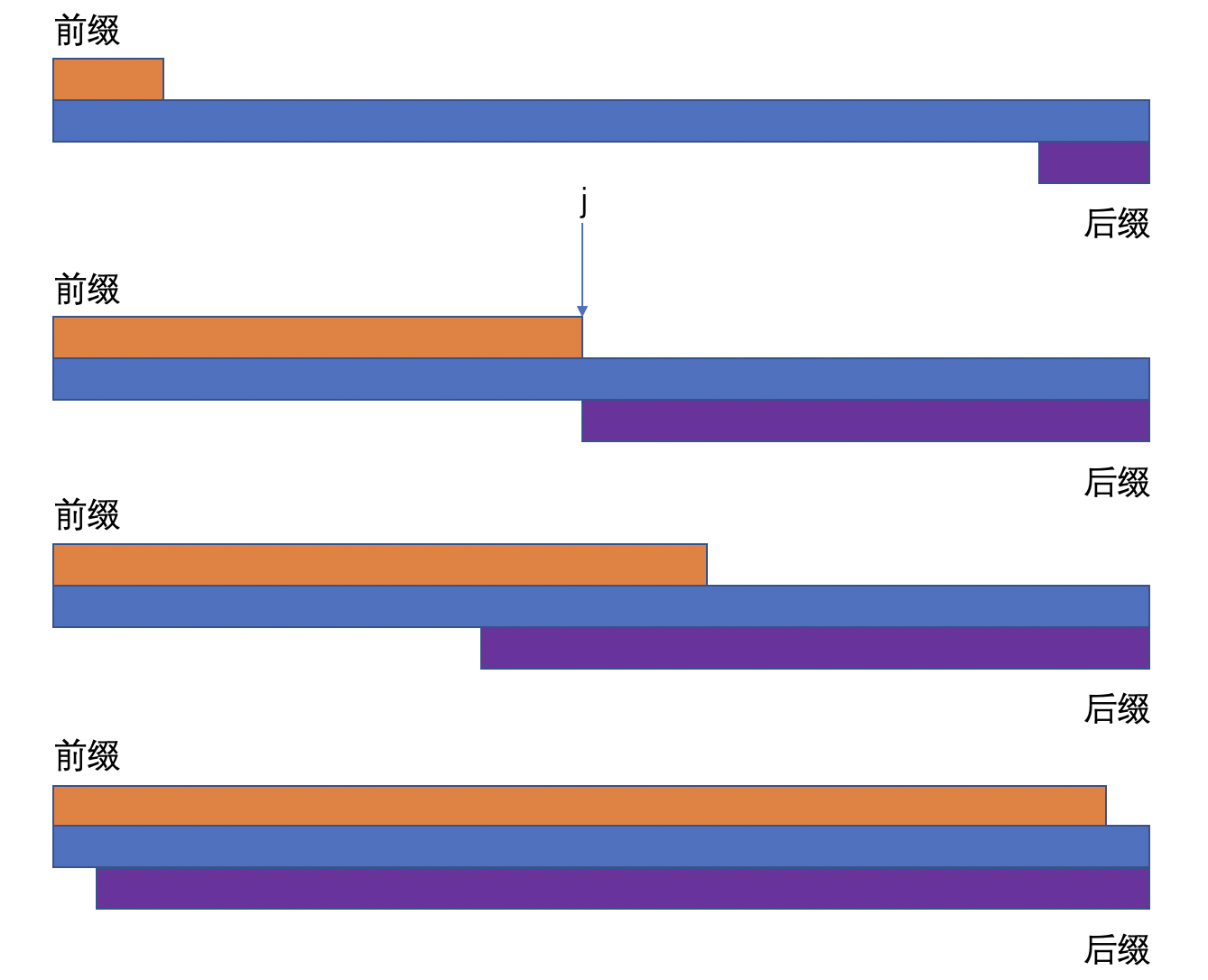
上述算法的比较次数为:1+2+3+...+(j+1)/2+...+j = O(j²)
这个方法效率不高,因此我们得采取另外的方案,接下来看看三位巨擘是怎么做的。
更好的这个方案是动态规划,主要是利用了回溯的思想。
在阅读下文之前,请先在心里面默念三遍next 数组保存的是子串的最长公共前后缀,加深一下大脑的认识。
下面我们来理解它是怎么样的一个流程:
数组next[X]指向的是前缀,i指向的是后缀,假设在某个时刻如下:
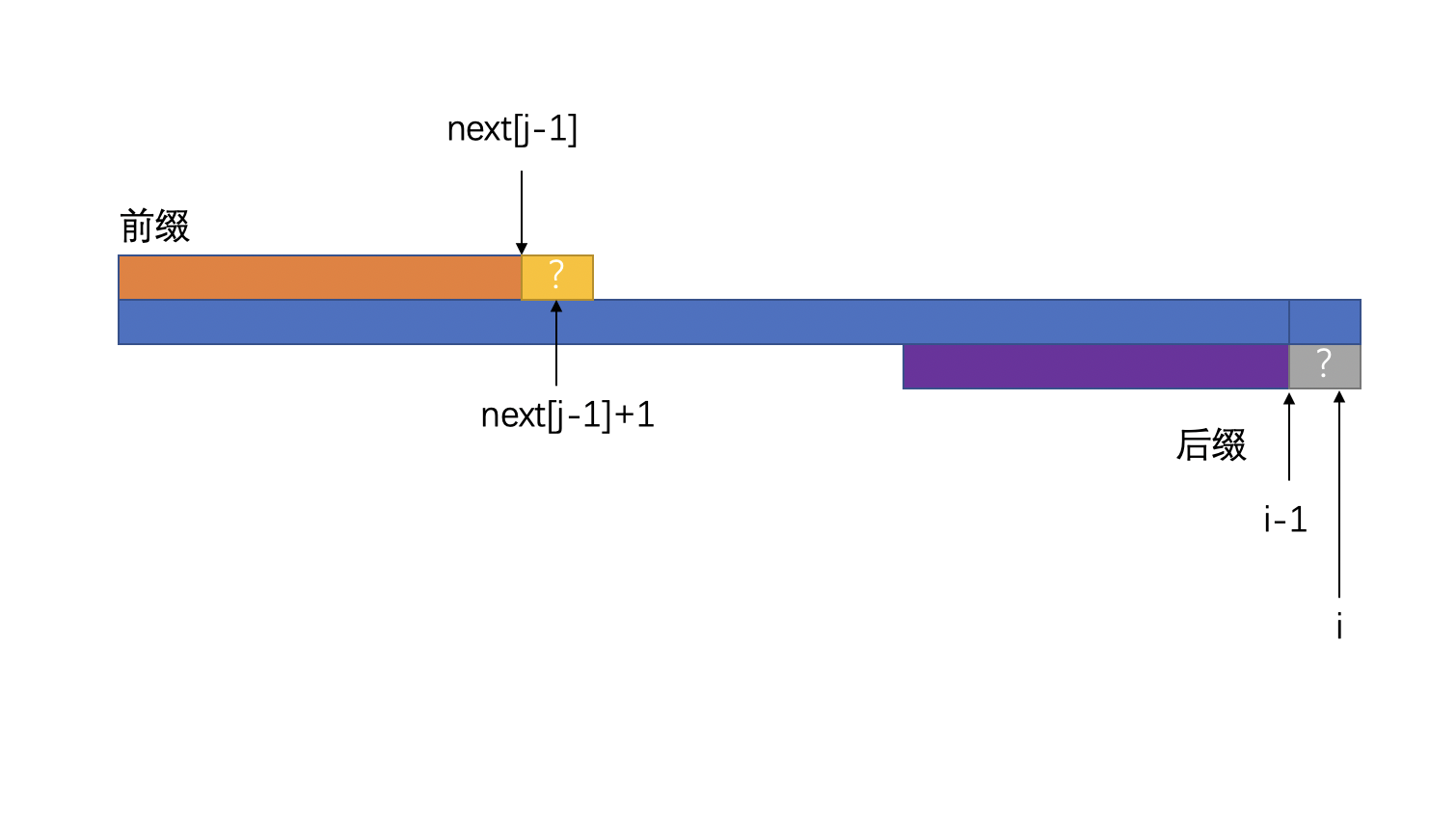
假设前面最长相同前缀为next[j-1],最长相同后缀是i-1这个位置,那么,如果next[j-1]+1这个位置和i这个位置上的字符相同的话,那我们至少可以粗略的得出一个结论:
next[j] >= next[j-1]+1。
有没有可能next[j] > next[j-1]+1呢?
我们先假设可能存在这样的情况
注意:下图中红色色块和蓝色色块并不是它们相等的意思,是描述这两个色块加入能否让next[j]变得更长。
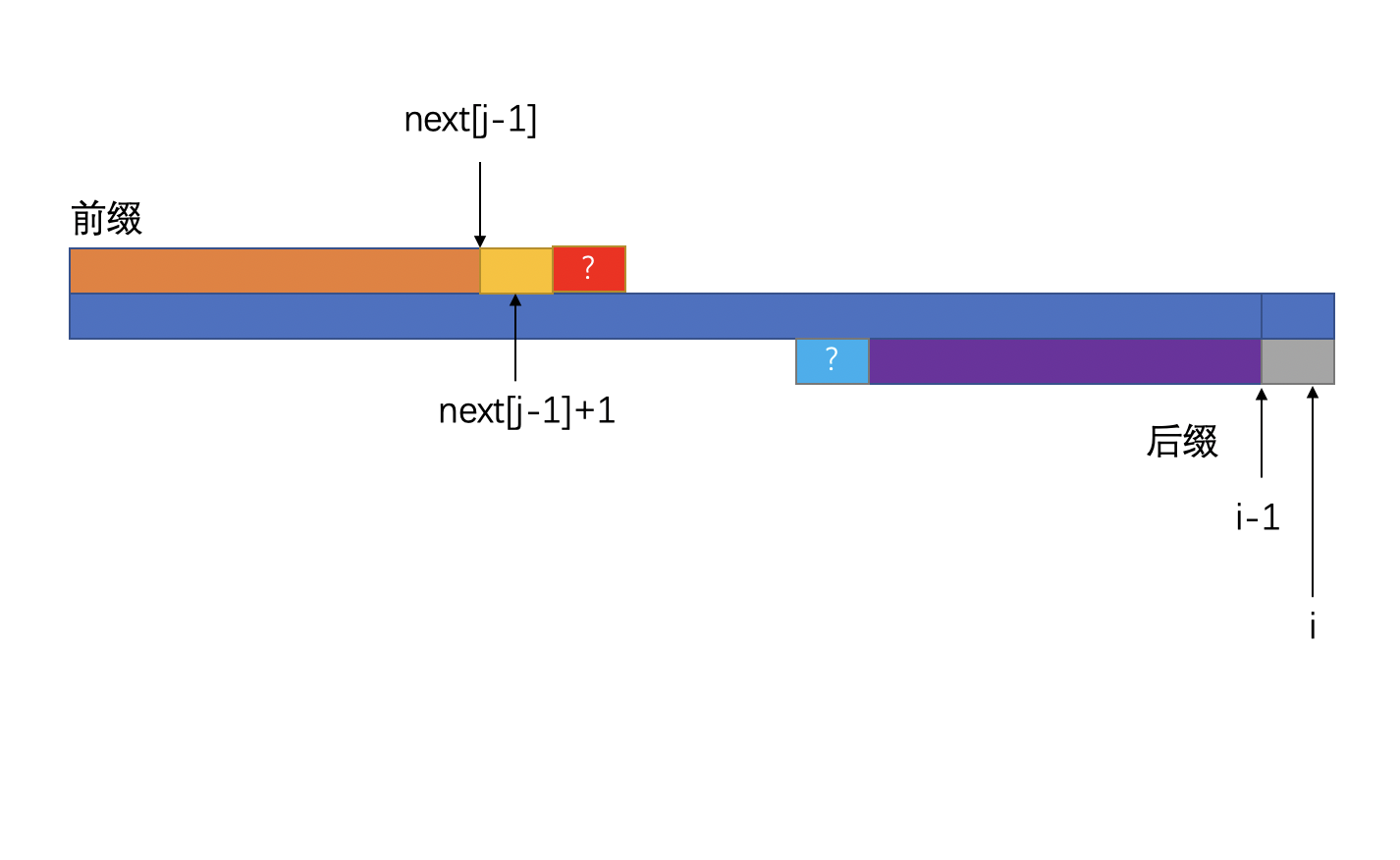
那么,根据假设,则应该存在:
两个蓝色的色块应该相等才对
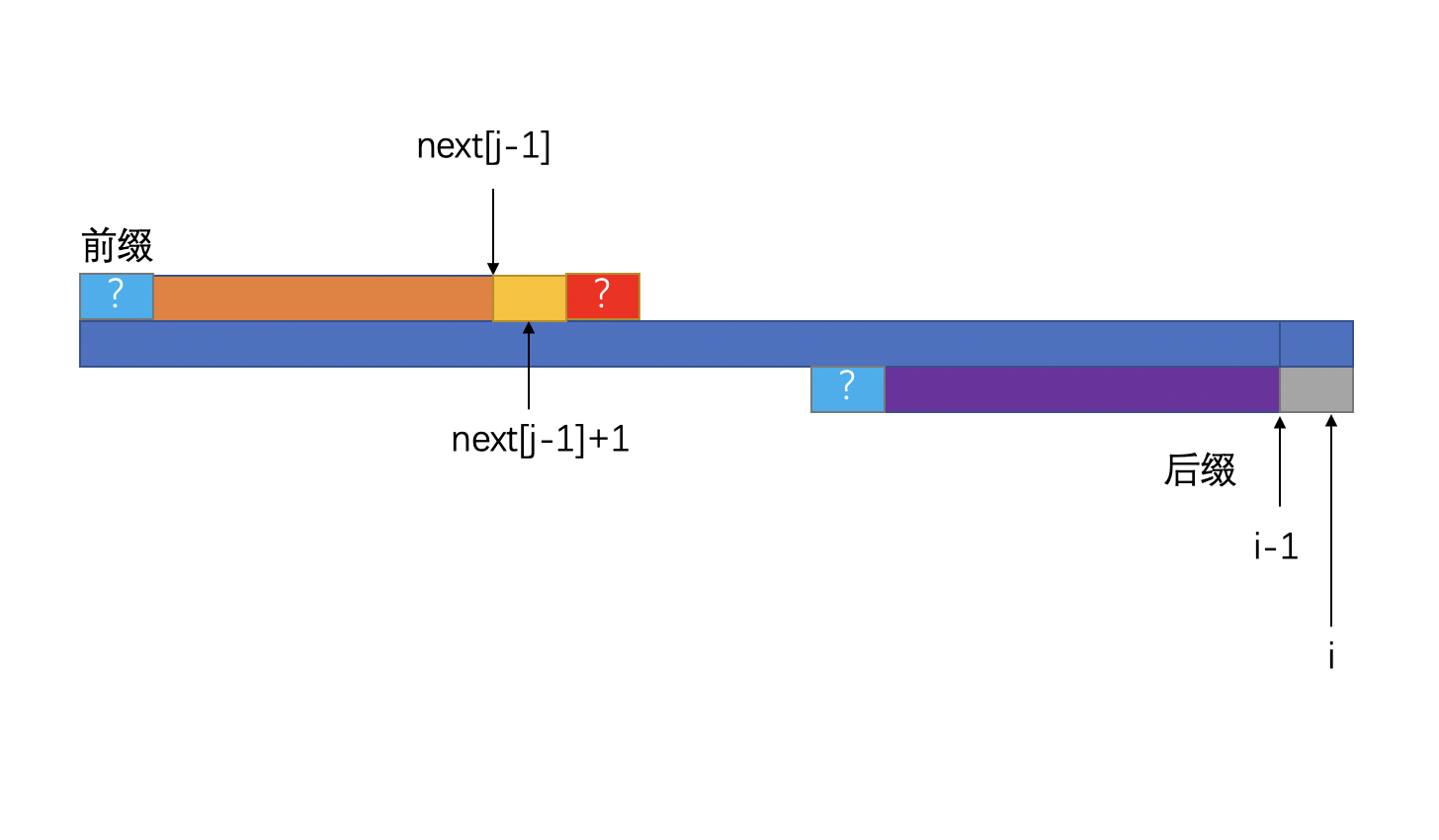
如这种场景:
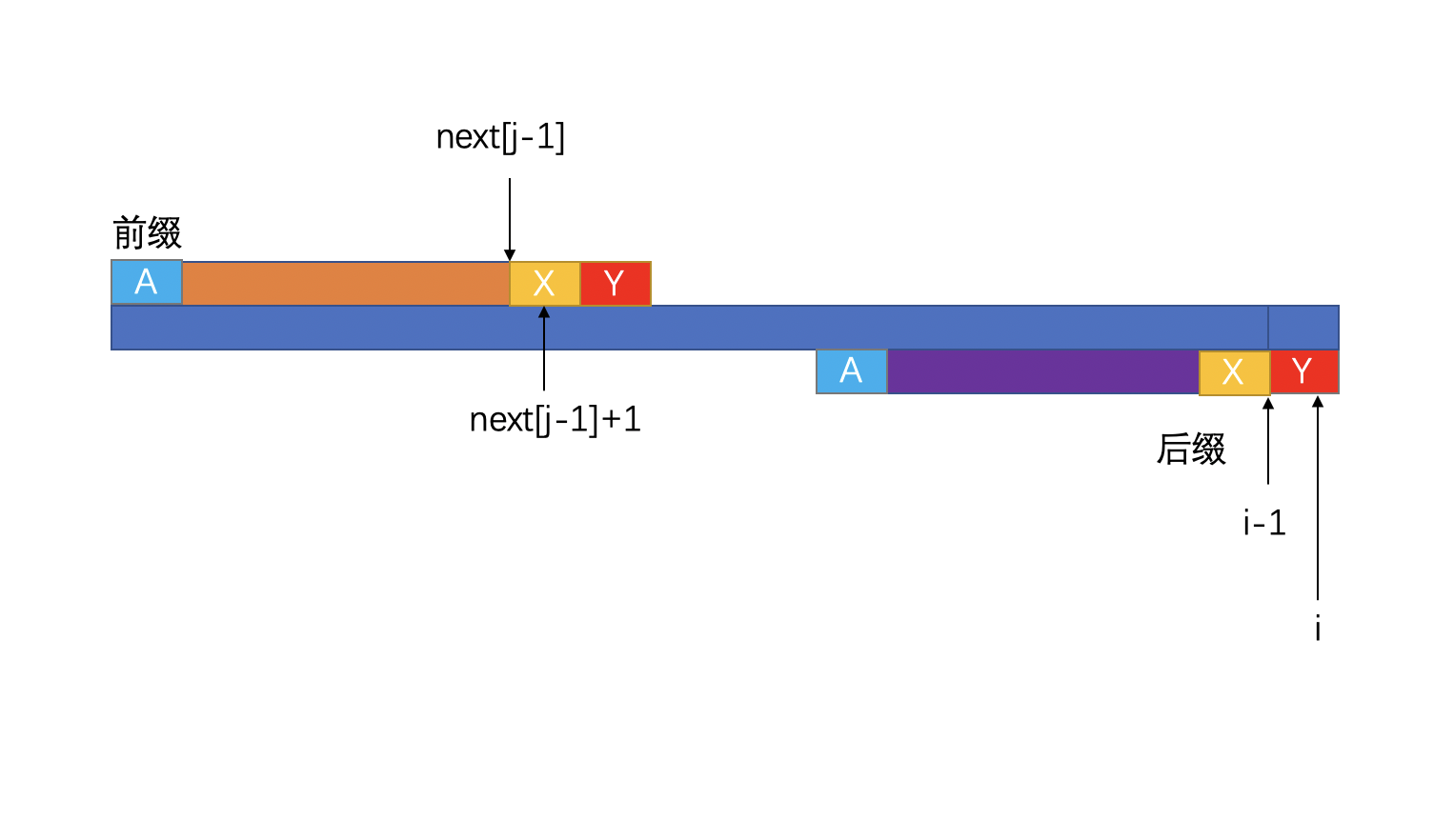
那么,对于长度为[0, i-1]的子串,最长公共前缀应该指向next[j-1] + 1才对,而不应该是指向next[j-1]。所以我们可以得出结论,每新增一个字符,最长公共前缀只有可能增加 1,即: next[j-1] + 1 = next[j]
上面我们讨论了匹配成功的情况,那么,如果失配呢?比如下图:
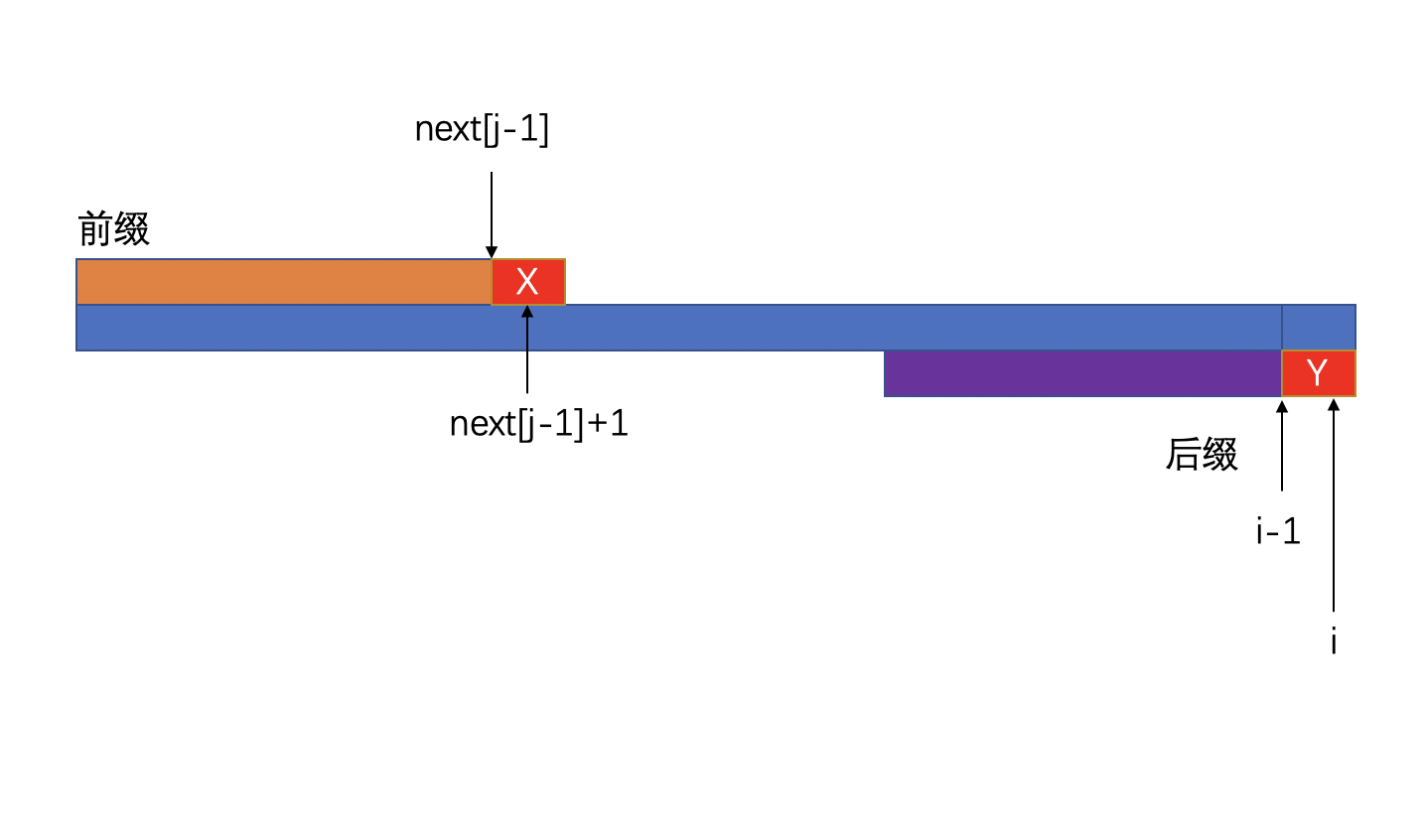
因为我们的 next[j-1]是一个递推计算的结果,我们此刻是能够知道next[next[j-1]]的。(想不明白的同学可以在此多思考一下,动态规划的问题本来就非常难以让人理解,想想刚才让你默念三遍的话)。
如下图所示:
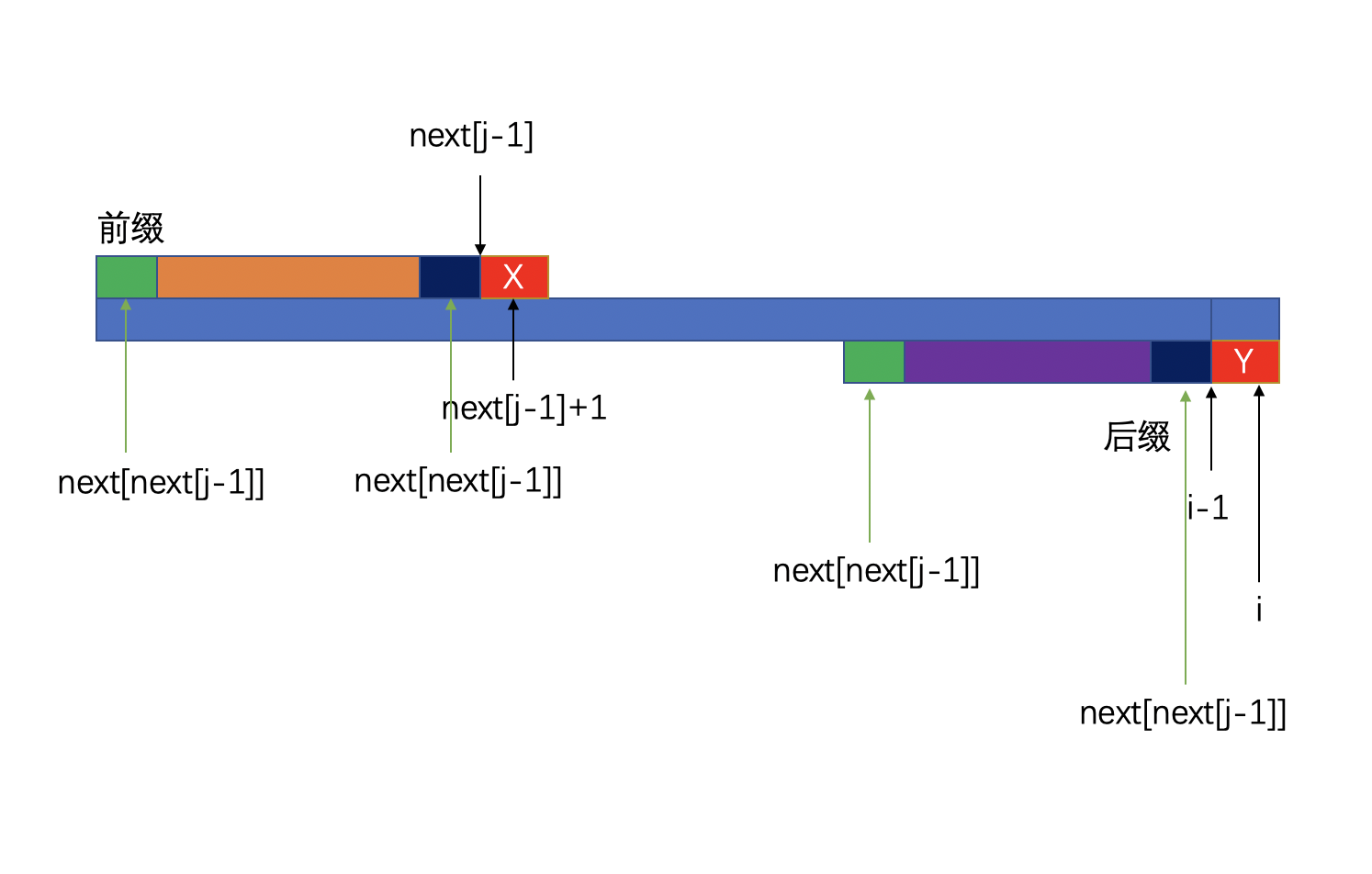
因此,我们可以回到如下状态重新开启匹配,如下图所示:
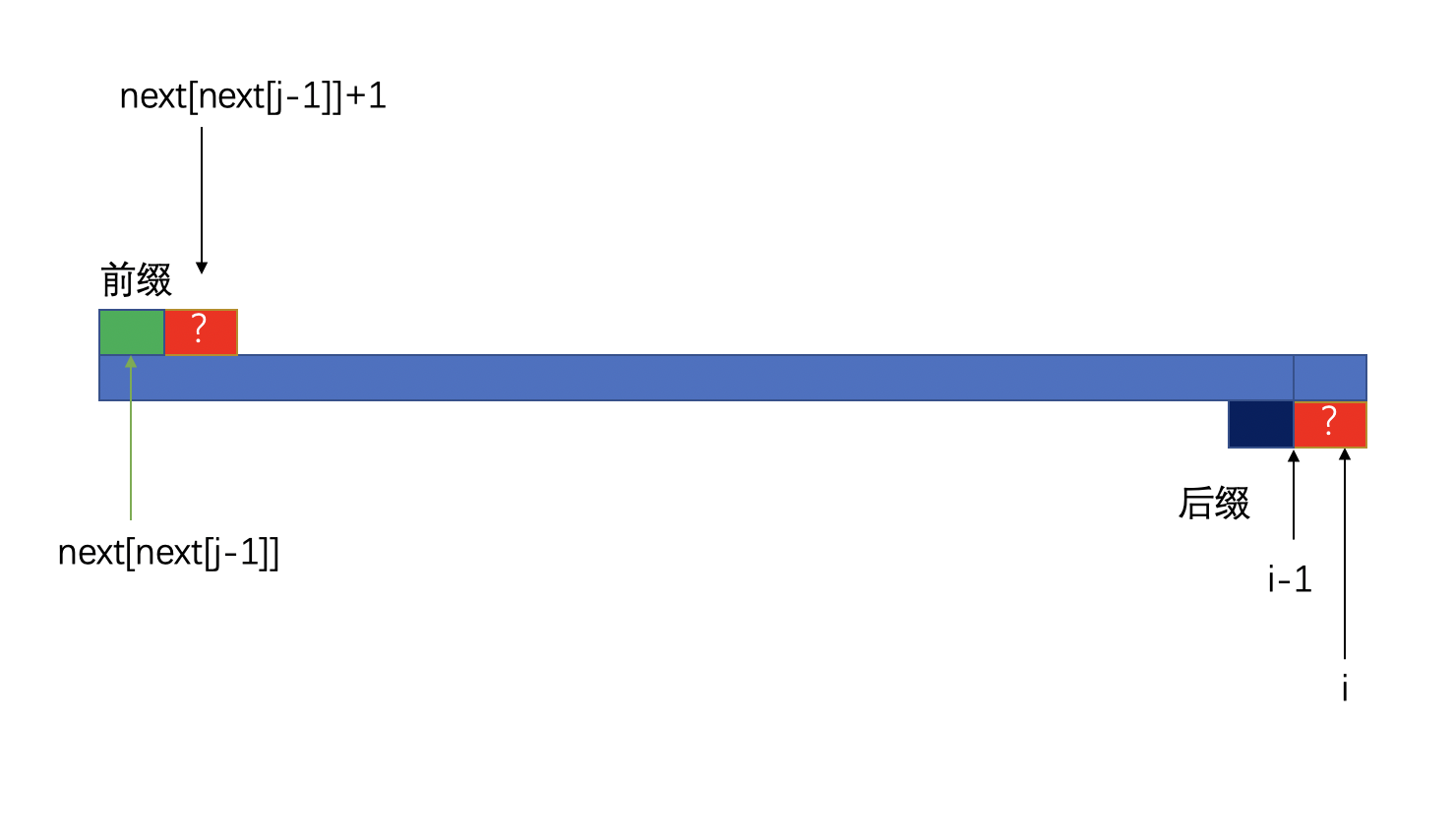
因此,又重复回到了我们刚才的流程。
这个解题思路非常复杂,它是回溯和动态规划思想的结合,一般回溯都会和递归挂钩,但是递归有时候会存在大量的重复计算,所以会考虑逆向思维将其转变为动规规划问题,这些都是算法里面较难且非常锻炼思维能力的章节(我个人感受是在面试中遇到动态规划算法题,就全靠你和公司的缘分了),这方面比较小白的朋友,可以尝试学习这门课程 (opens new window),相信你学过之后,再回头查看这篇博客,你会有新的理解。
整个求解next数组的算法的实现过程如下:
/**
* 生成next数组
* @param {String} pattern
* @param {Number[]} next
*/
function genNext(pattern) {
let m = pattern.length;
let next = [];
// 因为第一个字符串没有前后缀,所以可以直接赋值0,相当于动态规划可直接求得的初始条件
next[0] = 0;
//当取一个字符的时候,肯定是一个前后缀都没有的
for (let i = 1, j = 0; i < m; ++i) {
// 如果没有匹配到,递归的去求之前的最大前缀
// 退出循环条件是 k大于0 并且当前位置的字符串要是一样的
while (j > 0 && pattern[i] !== pattern[j]) {
// 回溯,找到上一次的最大前后缀的长度
j = next[j - 1];
}
// 如果匹配到了,最大的前后缀+1
if (pattern[i] == pattern[j]) {
j++;
}
// 求出当前字符串的最大公共前后缀,更新next数组
next[i] = j;
}
return next;
}
看到这儿,如果你全部都理解了的话,恭喜你,其实你已经掌握KMP算法了。
KMP算法搜索流程非常简单,其的实现如下:
/**
* KMP-Search
* @param {String} tpl
* @param {String} pattern
* @returns
*/
function kmpSearch(tpl, pattern) {
let n = tpl.length,
m = pattern.length;
let pos = -1;
let next = genNext(pattern);
for (let i = 0, q = 0; i < n; i++) {
/* 不断回溯,直到存在最长公共前后缀或回退到0,此处思路和求next数组求解思路一致。 */
while (q > 0 && pattern[q] != tpl[i]) {
q = next[q - 1];
}
// 如果当前字符和模式字符串指针位上的字符相等, 模式指针后移一位
if (pattern[q] == tpl[i]) {
q++;
}
/*
* 上述2个if不能交换位置,必须先判断是否匹配失败,才能继续进行匹配,如果交换的话,q指针先向后移动了一位,当前循环并没有结束,i指针还在前一个位置,此刻出现了错位,那么函数将不会正常运行。
*/
// 如果模式字符串指针的位置走到了最后一位,则说明匹配成功了
if (q == m) {
// 因为当前匹配的位置实际上是在pattern的length-1的位置上
pos = i - m + 1;
break;
}
}
return pos;
}
# KMP 的复杂度分析
在生成next数组的时候,我们看到是一个for循环和while循环嵌套,可以看到的是,每次j最坏退到0,但是只有在pattern[i] === pattern[j]的时候,j 才会递增的。j回退的总次数,是不会超过j增加的总次数的,最坏情况下,j累加的总次数是不会超过m的,所以while循环的执行次数是不会超过O(m)。所以生成next数组的时间复杂度是O(m)。在搜索过程中,同理。因此算法总的时间复杂度为 O(m+n),m 和 n 分别为两个字符串的长度;
因为生成next数组占用了一定的空间,所以空间复杂度为O(m),m 为子字符串的长度。