树的构建

1. 把后端返回的数据构建成树

这是一个很常见的操作，有些时候，是因为后端直接返回树结构的话，序列化时i/o开销比较大，在高并发场景下，会使得服务器的效率降低，因此不得不让前端自行构建树型结构的数据。

还有一种情况就比较搞笑了，这种情况一般出现在小公司，你的后端因为某些不可告人的秘密，告诉你只能给你返回数组。但是我们前端又必须需要一个树状结构。此时为了避免尴尬，前端可能会要求后端怎么样操作简单就怎么样约定数据格式了，然后前端按照相应的规格自己将其构建成树。

一般，后端给到前端的数据是这样的，我就以文件列表的例子来举例。

/**
 * 文件信息
 */
interface File {
  /**
   * 文件的ID，需要使用string类型，若使用number类型，当id特别大的时候，前端解析的结果将不正确
   */
  id: string;

  /**
   * 文件的父级ID, 可能不存在
   */
  pid: string | null;

  /**
   * 文件名
   */
  filename: string;

  /**
   * 文件类型，比如是文件还是文件夹
   */
  type: number;

  /**
   * 子文件列表
   */
  children?: File[];
}

方案 1 使用递归

/**
 * 构建文件树
 * @param file 文件信息
 * @param file 文件列表信息
 */
function buildTree(file: File, files: File[]) {
  // 找到当前文件的子文件列表
  let children = files.filter((fileEle: File) => {
    return fileEle.pid === file.id;
  });
  // 递归的处理当前文件子文件列表的子文件
  file.children =
    children.length === 0
      ? undefined
      : children.map((subFile: File) => buildTree(subFile, files));
  return file;
}

/**
 * 将文件列表转为文件树，并且返回根节点
 * @param files 文件列表
 */
function build(files: File[]) {
  // 构建结果
  const roots = files
    .filter((file) => {
      // 这一步操作是为了找到所有的根节点
      return file.pid === null;
    })
    .map((file) => {
      // 对根节点的数据进行构建
      return buildTree(file, files);
    });
  return roots;
}

方案 2 使用哈希表

这个方案是有点儿取巧的一种做法了，因为其完美的利用了引用类型数据的特征，因为引用数据类型，大家都同时持有一块相同的内存区域，不同的人对它进行修改，都会在它的身上得到体现。

/**
 * 将文件列表转换成为哈希表
 * @param {File[]} files
 */
function makeHashMap(files) {
  const map = new Map();
  files.forEach((file) => {
    // 以ID为主键建立哈希映射
    map.set(file.id, file);
  });
  return map;
}

function buildTree(files) {
  // 将文件构建成哈希表，主要是为了后续的查找方便
  const fileMap = makeHashMap(files);
  const roots = [];
  // 逐个的对每个文件增加子元素
  files.forEach((file) => {
    // 找父级文件，如果找不到的话，说明是根节点
    const parentFile = fileMap.get(file.pid);
    if (parentFile) {
      if (!Array.isArray(parentFile.children)) {
        parentFile.children = [file];
      } else {
        parentFile.children.push(file);
      }
    } else {
      roots.push(file);
    }
  });
  // 最后只需要找出根节点的文件列表即可完成构建
  return roots;
}

2. 从二叉树的两个遍历序列构建二叉树

通过无重复值的二叉树遍历中序序列+先序（或后序）序列能唯一确定一颗二叉树。

注意事项

仅凭先序和后序序列无法唯一确定一颗二叉树。

先序序列的第一个节点一定是根节点，然后我们就可以通过这个根节点，在中序序列中确定其根节点的位置。一旦确定了中序序列的根节点位置，那就可以得到左子树序列和右子树序列。而同一颗二叉树的左右子树序列长度是相同的，因此，我们可以根据从中序序列获取到的左右子树片段，找出先序序列的左右子树片段。重复这个过程，直到构建完成。

后序序列+中序序列构建思路还先序序列+中序序列构建思路类似。

通过先序序列+中序序列构建二叉树

二叉树结构定义如下：

interface TreeNode<T> {
  left: TreeNode<T> | null;
  right: TreeNode<T> | null;
  val: T;
}

算法实现如下：

/**
 * 从二叉树的先序序列+中序序列构建二叉树
 * @param {number[]} preorder 先序序列
 * @param {number[]} inorder 中序序列
 * @return {TreeNode}
 */
var buildTree = function (preorder, inorder) {
  if (
    !Array.isArray(preorder) ||
    preorder.length === 0 ||
    !Array.isArray(inorder) ||
    inorder.length === 0 ||
    preorder.length != inorder.length
  ) {
    return null;
  }
  let rootVal = preorder[0];
  // 在中序遍历的结果中找到根节点所在的位置，则【0，idx】的是左子树，【idx+1，length】的是右子树
  let rootNodeIdx = inorder.findIndex((x) => x === rootVal);
  let inLeftSubtreeNodes = inorder.slice(0, rootNodeIdx);
  let inRightSubtreeNodes = inorder.slice(rootNodeIdx + 1);
  // 在先序遍历的结果中提取对应长度的的子集 可以得到对应的左子树结果集合
  let preLeftSubtreeNodes = preorder.slice(1, inLeftSubtreeNodes.length + 1);
  // 继续在先序遍历的结果中提取对应长度的子集，可以得到对应右子树结果集合
  let preRightSubtreeNodes = preorder.slice(1 + inLeftSubtreeNodes.length);
  return {
    val: rootVal,
    left: buildTree(preLeftSubtreeNodes, inLeftSubtreeNodes),
    right: buildTree(preRightSubtreeNodes, inRightSubtreeNodes),
  };
};

通过后序序列+中序序列构建二叉树

算法实现如下：

/**
 * 通过后序序列+中序序列构建二叉树
 * @param {number[]} inorder
 * @param {number[]} postorder
 * @return {TreeNode}
 */
var buildTree = function (inorder, postorder) {
  if (
    !Array.isArray(inorder) ||
    inorder.length === 0 ||
    !Array.isArray(postorder) ||
    postorder.length === 0 ||
    inorder.length != postorder.length
  ) {
    return null;
  }
  let len = postorder.length;
  let rootVal = postorder[len - 1];
  // 在中序遍历的结果中找到根节点所在的位置，则【0，idx】的是左子树，【idx+1，length】的是右子树
  let rootNodeIdx = inorder.findIndex((x) => x === rootVal);
  let inLeftSubtreeNodes = inorder.slice(0, rootNodeIdx);
  let inRightSubtreeNodes = inorder.slice(rootNodeIdx + 1);
  // 在后序遍历的结果中提取对应长度的的子集 可以得到对应的左子树结果集合
  let posLeftSubtreeNodes = postorder.slice(0, inLeftSubtreeNodes.length);
  // 继续在后序遍历的结果中提取对应长度的子集，可以得到对应右子树结果集合
  let postRightSubtreeNodes = postorder.slice(
    posLeftSubtreeNodes.length,
    postorder.length - 1
  );
  return {
    val: rootVal,
    left: buildTree(inLeftSubtreeNodes, posLeftSubtreeNodes),
    right: buildTree(inRightSubtreeNodes, postRightSubtreeNodes),
  };
};

为什么同一颗二叉树的先序序列+后序序列不能唯一确定一颗二叉树呢，我们通过举反例来证明这个结论。

假设我们有一个二叉树的先序序列 ABC，一个后序序列 CBA

那么，能够得到 ABC 先序序列的可能的二叉树如下：

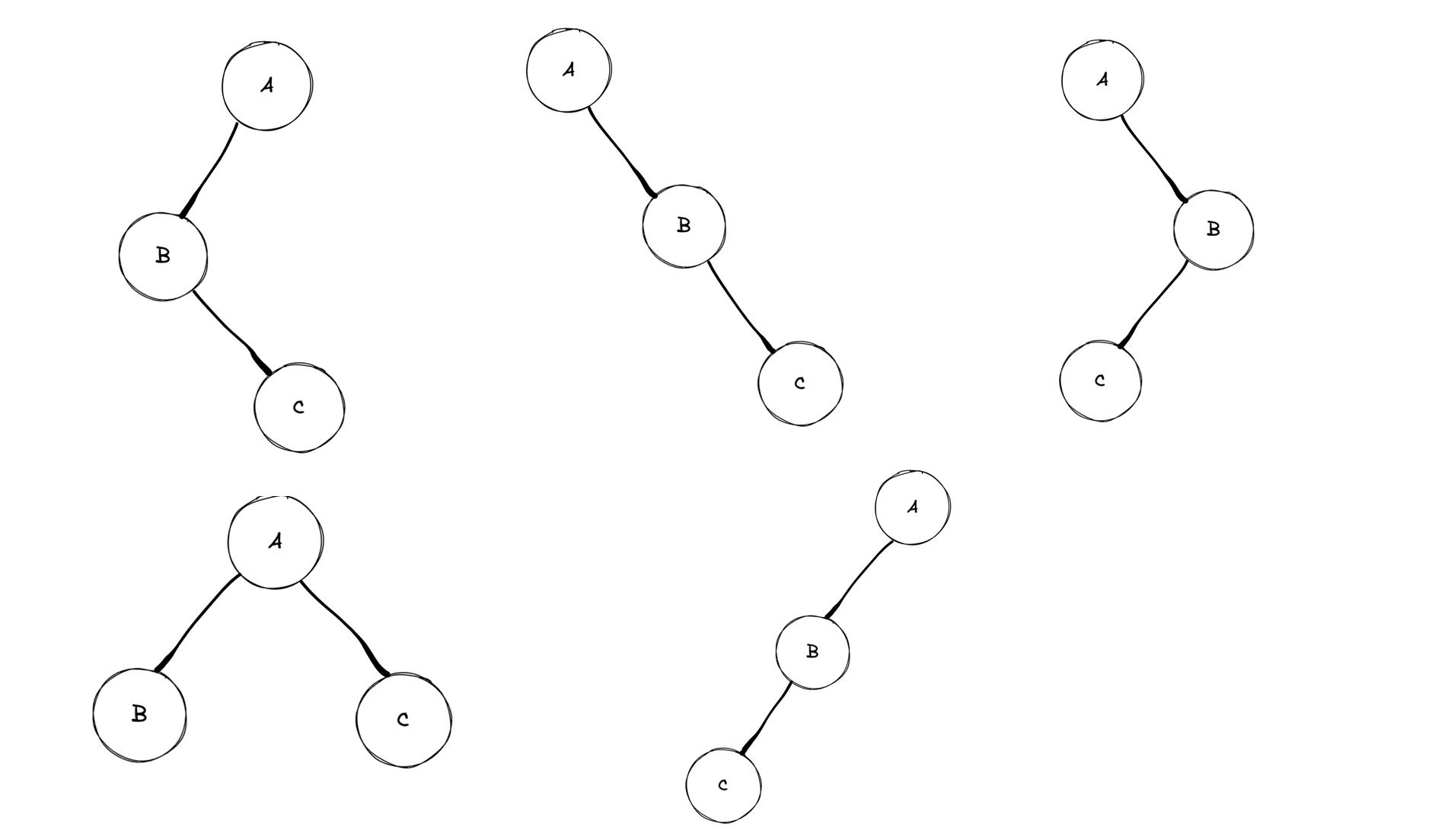
那么，能够得到 CBA 后续序列可能的二叉树如下：

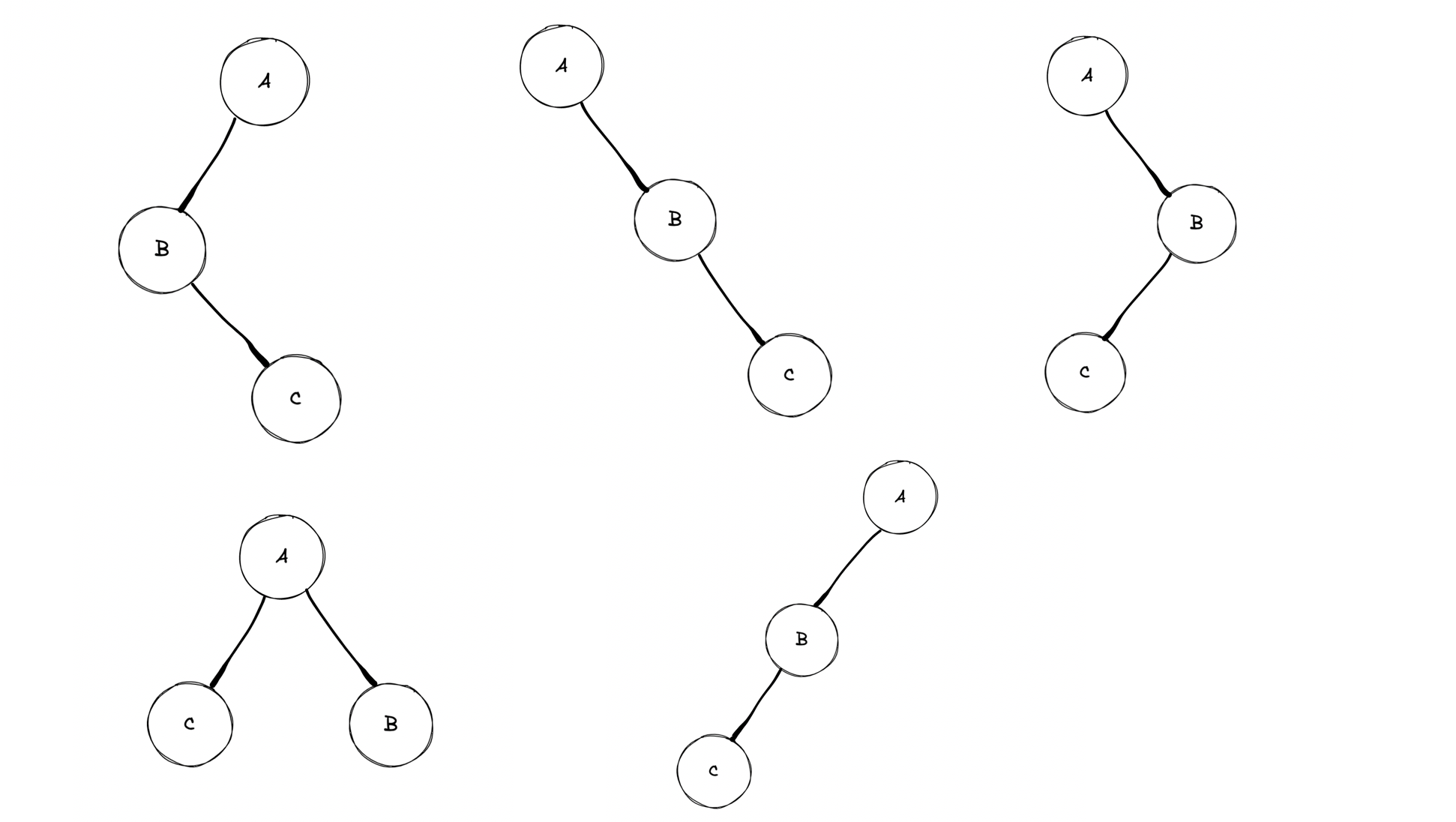
可以看到，同一颗二叉树的先序和后序序列，但是可以构造出不同的二叉树。