# 1.算法好坏的衡量依据——复杂度
# 时间复杂度
算法的时间复杂度T(n),是一个用于度量一个算法的运算时间的一个描述,本质是一个函数,根据这个函数能在不用具体的测试数据来测试的情况下,粗略地估计算法的执行效率,换句话讲时间复杂度表示的只是代码执行时间随数据规模增长的变化趋势。
举个大家非常熟悉的冒泡排序的一个例子:
/**
* 对数组进行冒泡排序
* @param {Array<number>} arr 需要进行排序的数组
*/
function bubbleSort(arr) {
let temp = null;
// 外层循环变量i 用于控制参与排序数据的规模
for (let i = arr.length - 1; i >= 0; i--) {
// 定义标记,用于判断本轮是否参与交换
let flag = true;
// 内层循环用于把最“重”的元素下沉至非有序片段的最后一位
for (let j = 0; j < i; j++) {
// 注意冒泡排序是两两相邻的比较
if (arr[j] > arr[j + 1]) {
temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
// 如果交换了元素,还需要设置标记,若数组已经有序,可以提前终止排序,提升性能
flag = false;
}
}
// 如果说没有参与交换,则认为数组已经有序,则可以完成排序
if (flag) {
break;
}
}
}
举一个极端的例子,假设现在输入的数据是从大到小的,大家现在可以看到,上面的算法是对数据进行升序排序。
对于程序里面的赋值,算术运算,位运算,数组寻址等操作,这是编程语言提供给我们的能力,我们已经无法提升它的速度了,所以这些操作都是常数级的操作。
第一步: 把 0 这个位置上的数据挪动到最后一个位置上,需要进行 2*N 次交换
第二步: 把 0 这个位置上的数据挪动到倒数第二个位置上,需要进行 2*N-1 次交换
重复以上操作,
第 N-1 步:把 0 这个位置交换到 1 这个位置上,需要执行 2 次操作
根据高中学过的等差数列前 N 项和公式,我们可以得到一个粗略的结果为 a*N²+b*N+c,当 N 在特别大的时候,b*N + c 其实对结果的影响不大。
而我们并不需要一个精确的次数,只是想得到一个描述其复杂度规模的指标,因此,系数 a 也可以省略。
所以,最终我们推导出来,冒泡排序的算法时间复杂度是O(N²);
下面是我在网上随便找的一个常见的时间复杂度的对比图,大家看一下,对不同的时间复杂度的规模有一个认识。
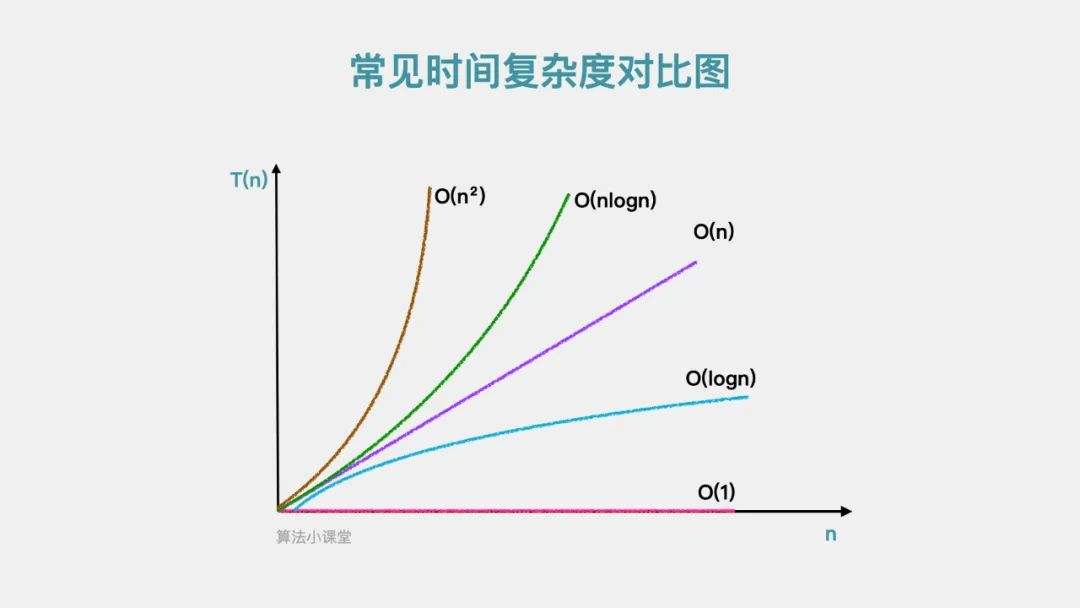
所有常数级的操作都是O(1),正常的一轮循环是O(n),像二分查找,平衡二叉树,跳跃链表的查找,堆的插入,每次运算之后都会使得数据的规模减半,这类操作的复杂度是O(log n),(至于这个O(log n)是怎么算出来的,举个例子:比如 2 的 10 次方是 1024,那么我们对 1024 进行减半得到一个新的值,然后再对这个新值减半,重复这个操作,到得到的数不能再继续减半为止,最多只能操作 10 次,因此求得二分查找的时间复杂度是O(log n)),像冒泡排序,选择排序,插入排序这类简单排序算法,都是简单的两个循环相叠加,这类操作的时间复杂度是O(n²),比如像堆排序,归并排序,快速排序这类复杂的排序算法,由于里面有运用分治或折半查找思想的优化,这类排序算法的时间复杂度为 O(n*log n)。
正常我们的实际开发中很少遇到O(n³)及以上复杂度的操作,如果出现了此类情况,请一定要检查一下自己的思维方式是否错误。因为我曾经刚毕业的时候,在有一次算股票的成交均线的时候,就把一个O(n)级别的复杂度计算写成了O(n的n次方)级别的计算,这种错误一旦在数据量比较大的时候,会严重影响用户使用的体验,如果用户无法忍受,怒删程序,会造成公司的活跃用户损失,那有可能会影响到你的绩效了哟。
# 空间复杂度
算法的空间复杂度 S(n)定义为该算法所耗费的存储空间,它也是问题规模 n 的函数,也是描述代码占用空间随数据规模增长的变化趋势。
比如我们定义一个变量,这时计算机就会为我们开辟一个内存空间用于存储它。跟时间复杂度的计算类似,因为我们不同语言特定的数据类型占用的内存大小是明确的,我们是无法优化的。
就比如,我们做一次哈希映射,我们需要建立起一个对这个数据的关系,这种操作就是O(1),比如你需要将一个数组的数据都做一份映射,归并排序时需要额外开辟一个数组用于归并数据,那么此时我们的空间复杂度就是O(N)。