图

在我们日常生活中，线性表表示一对一的关系，树表示一对多的关系，图表示的是多对多的关系，线性表和树相当于是图的子集。

图是我们现实生活中连接关系的抽象，例如朋友圈、微博的关注关系，互联网的连接等。

在前端的实际开发中，如果当你遇到和流程图相关的业务时，可能会用到图；若你从事和地图相关的业务，那可能你得天天和图打交道了。

图中的概念

图中的专业术语特别的多，我们只列一些在实际开发中可能会用到的一些关键词。

图中的两点如果存在权重的话，则称为带权图，图的两个顶点中间如果不存在方向的话，则称为无向图，有向的话则称为有向图

对于图中任意一个顶点与该顶点相关联的边的条数，称为图的度；

对于有向图来说的话，从顶点引出的边叫它的出度，别的顶点指向它的边叫做它的入度。

在无向图中，如果从顶点 vi 到顶点 vj 有路径，则称 vi 和 vj 连通，如果图中任意两个顶点之间都连通，则称该图为连通图，否则，将其中的极大连通子图称为连通分量。（我觉得用同俗易懂的语言来理解这个概念就是说这个图里面是否有一个或几个顶点单着呢。）

在有向图中，如果对于每一对顶点 vi 和 vj，从 vi 到 vj 和从 vj 到 vi 都有路径，则称该图为强连通图；否则，将其中的极大连通子图称为强连通分量。

目前我在实际开发中所用到的关于图的名词就如上所述，对于图有兴趣的同学，可以自行查阅相关资料。

图在计算机中的表示

首先，大家一定不要拘泥于老师所讲述的邻接矩阵和邻接表的表示方法。曾经我就是对老师所授内容囫囵吞枣，导致理解上产生了偏差。只要你能够表示逻辑的关系（不管是一对一，多对一还是多对多），只要你的这个标识方法能够最快的解决你的问题，那就是一个好的表示方法。

举个前端实际开发中的例子，像一个对象中可能存在一个或者多个循环引用，那就是图。

但是，我们还是需要讲一下图的两种最常见的表示法：邻接矩阵和邻接表法。

对于下面这个图，我们分别尝试用邻接矩阵和邻接表来表示它。

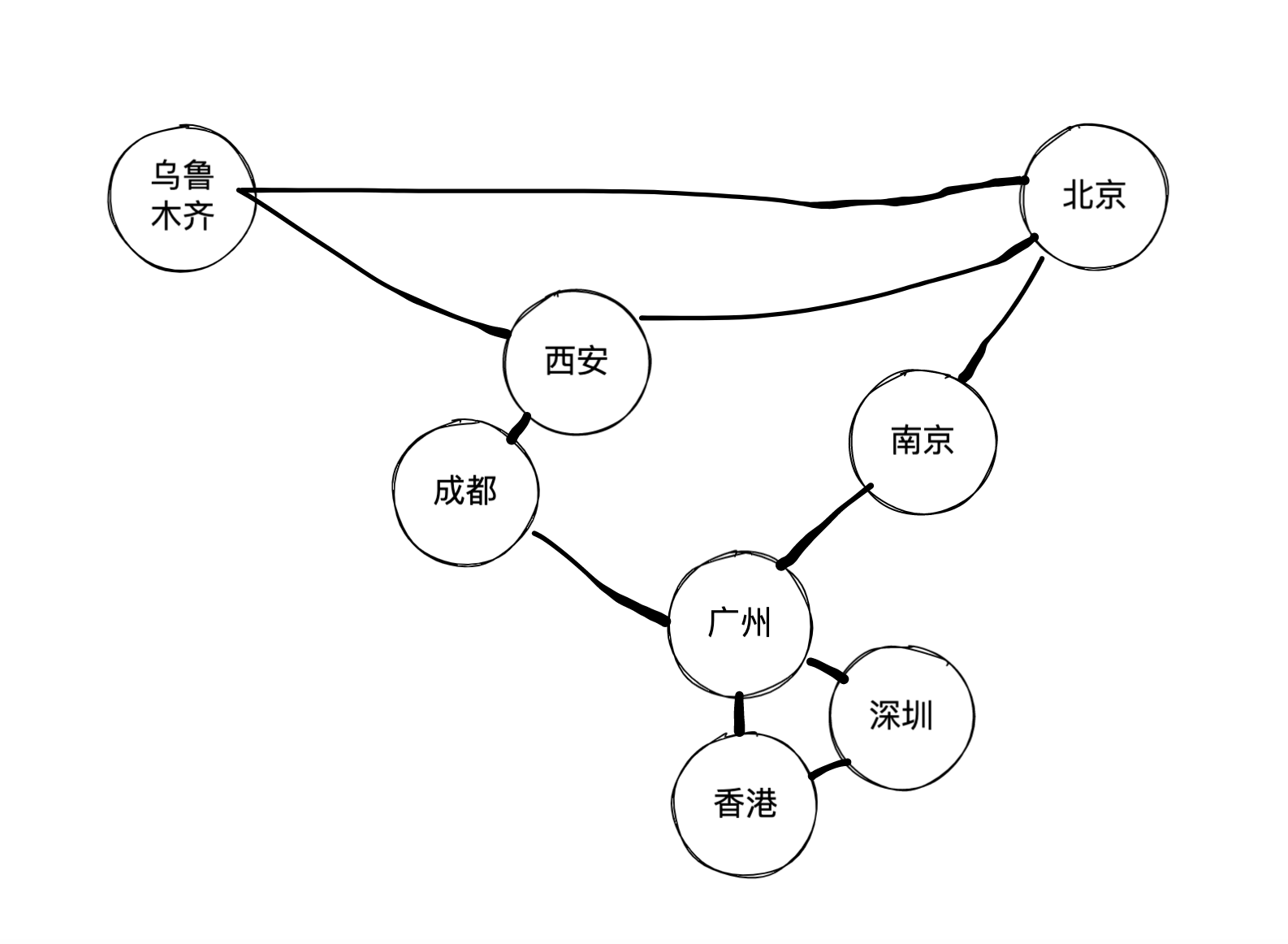
我们对这些城市分别编个号

const cities = [
  "北京",
  "南京",
  "广州",
  "深圳",
  "香港",
  "成都",
  "西安",
  "乌鲁木齐",
];

邻接矩阵表示法

一个二维数组，数组的长度和宽度为图的顶点数，若两点之间存在路径，则matrix[i][j]不为零，否则为零。

对角线全部为 0，因为城市不需要自己和自己连接

北京和南京存在连接，则 matrix[0][1]=1，matrix[1][0] = 1，因为我们是无向图，如果想表达仅可以从北京到南京，则matrix[0][1]=1

南京和广州存在连接，matrix[1][2]=1，matrix[2][1] = 1

深圳和广州存在连接，matrix[3][2]=1，matrix[2][3] = 1

深圳和香港存在连接，matrix[3][4]=1，matrix[4][3] = 1

广州和香港存在连接，matrix[2][4]=1，matrix[4][2] = 1

广州和成都存在连接，matrix[2][5]=1，matrix[5][2] = 1

西安和成都存在连接，matrix[5][6]=1，matrix[6][5] = 1

西安和乌鲁木齐存在连接，matrix[6][7]=1，matrix[7][6] = 1

西安和北京存在连接，matrix[0][7]=1，matrix[7][0] = 1

[
  [0, 1, 0, 0, 0, 0, 0, 1],
  [1, 0, 0, 1, 1, 1, 0, 0],
  [0, 0, 0, 0, 0, 0, 0, 0],
  [0, 1, 0, 0, 1, 0, 0, 0],
  [0, 1, 0, 1, 0, 0, 0, 0],
  [0, 1, 0, 0, 0, 0, 1, 0],
  [0, 0, 0, 0, 0, 1, 0, 1],
  [1, 0, 0, 0, 0, 0, 1, 0],
];

若两点之间需要表示权重，需要将 1 改为权重即可。

邻接表表示法

一个一维数组，数组的每个元素为一个链表，链表指向当前顶点的所有邻接点。

interface Vertex {
  cityName: string;
  next: Vertex | null;
}

[
  {
    cityName: "北京",
    next: {
      cityName: "西安",
      next: {
        cityName: "南京",
        next: {
          cityName: "乌鲁木齐",
          next: null,
        },
      },
    },
  },
  {
    cityName: "南京",
    next: {
      cityName: "北京",
      next: {
        cityName: "广州",
        next: null,
      },
    },
  },
  {
    cityName: "广州",
    next: {
      cityName: "成都",
      next: {
        cityName: "南京",
        next: {
          cityName: "深圳",
          next: null,
        },
      },
    },
  },
  {
    cityName: "香港",
    next: {
      cityName: "深圳",
      next: {
        cityName: "广州",
        next: null,
      },
    },
  },
  {
    cityName: "深圳",
    next: {
      cityName: "广州",
      next: {
        cityName: "香港",
        next: null,
      },
    },
  },
  {
    cityName: "成都",
    next: {
      cityName: "西安",
      next: {
        cityName: "广州",
        next: null,
      },
    },
  },
  {
    cityName: "西安",
    next: {
      cityName: "成都",
      next: {
        cityName: "北京",
        next: {
          cityName: "乌鲁木齐",
          next: null,
        },
      },
    },
  },
  {
    cityName: "乌鲁木齐",
    next: {
      cityName: "西安",
      next: {
        cityName: "北京",
        next: null,
      },
    },
  },
];

使用邻接表表示，若两点之间需要表示权重，还需要额外在链表节点增加一个域用以表示权重。

上面两种表示法都把同一条边存了 2 次的，我们也之前也介绍了，图的表示方法有很多种，选择一种适合你的就好，接下来我介绍一下我个人在开发中的表示法。 首先定义图和顶点

class Edge {
  constructor(name) {
    this.name = name;
  }
  /**
   * 边的编号
   */
  name;
  /**
   * 起始点
   * @type {Vertex}
   */
  from;
  /**
   * 终止点
   * @type {Vertex}
   */
  to;
}

class Vertex {
  /**
   * 城市名称
   */
  cityName;
  /**
   * 邻接点
   */
  siblings = [];
  constructor(cityName) {
    this.cityName = cityName;
  }
}

class Graph {
  vertexList = [];
  edgeList = [];
  addVertex(v) {
    this.vertexList.push(v);
  }

  /**
   * 增加边
   * @param {Vertex} from
   * @param {Vertex} to
   */
  addEdge(from, to) {
    const name = `${from.cityName}至${to.cityName}`;
    const edge = new Edge(name);
    this.edgeList.push(edge);
    from.siblings.push(to);
    to.siblings.push(from);
  }
}

接着，初始化数据：

const g = new Graph();
const beijing = new Vertex("北京");
const nanjing = new Vertex("南京");
const guangzhou = new Vertex("广州");
const shenzhen = new Vertex("深圳");
const hongkong = new Vertex("香港");
const chengdu = new Vertex("成都");
const xian = new Vertex("西安");
const urumchi = new Vertex("乌鲁木齐");

/**
 * 将城市加入到图中
 */
g.addVertex(beijing);
g.addVertex(nanjing);
g.addVertex(guangzhou);
g.addVertex(shenzhen);
g.addVertex(hongkong);
g.addVertex(chengdu);
g.addVertex(xian);
g.addVertex(urumchi);
/**
 * 建立连接关系
 */
g.addEdge(beijing, nanjing);
g.addEdge(beijing, xian);
g.addEdge(nanjing, guangzhou);
g.addEdge(guangzhou, shenzhen);
g.addEdge(guangzhou, hongkong);
g.addEdge(hongkong, shenzhen);
g.addEdge(chengdu, guangzhou);
g.addEdge(chengdu, xian);
g.addEdge(urumchi, xian);
g.addEdge(urumchi, beijing);

上述这种方法是大家在实际开发中最可能用到的。后面，一些图的算法，我们还会基于这个例子阐述。