拓扑排序

拓扑排序（Topological Sorting）是一种图论算法，用于解决有向无环图（DAG，Directed Acyclic Graph）中的节点排序问题。拓扑排序的目标是将图中的所有节点按照一种线性顺序排列，使得对于任何有向边 (u, v)，节点 u 在排列中都出现在节点 v 的前面。

换句话说，拓扑排序能够找到一种排列，使得所有的依赖关系都能够被满足。

拓扑排序常常用于解决涉及依赖关系的问题，如编译顺序、任务调度、课程选修等。

如果有向图中存在环路（循环依赖），则无法进行拓扑排序，因为无法满足依赖关系。

从拓扑排序的用途的阐述，我们可以得知，前端程序员似乎每天都在应用它，如果你还没有想到？你是不是忽略了一个非常重要的知识点，当你在命令行输入npm install之后，是不是就是经历了上述所说的过程。

拓扑排序的思路

对于一个有向无环图，肯定有一些顶点是没有入度的，也就是说这些顶点没有前驱依赖，那么这些顶点就可以直接输出来了，但是将这些顶点处理完成之后，这些顶点的后继节点的入度肯定要相应的减 1，重复这个过程，我们再看一下还有没有入度为 0 的顶点，直到处理完所有的顶点

假设图内存在环的话，那就是意味着一些顶点的入度永远无法变为 0，那就意味着我们最终处理的结果的顶点数肯定是比图的定点数少的。

对于怎么处理入度为 0 的顶点，我们可以把它放到一个专门的地方，每次都从这个专门的地方取一个顶点出来进行处理，输出这个顶点之后，扫一下它的邻接点，如果发现了有入度为 0 的节点，又可以将其加到这个队列，直到没有满足条件的顶点。

拓扑排序的算法实现

为了方便直观，我以以下结构来描述DAG。

/**
 * 图中的顶点
 */
export interface Vertex {
  /**
   * 入度
   */
  inDegree: Edge[];
  /**
   * 出度
   */
  outDegree: Edge[];
  /**
   * 节点名称
   */
  name: string;
}

/**
 * 图中的边
 */
export interface Edge {
  /**
   * 权重
   */
  weight?: number;
  /**
   * 前驱节点
   */
  prev: Vertex;
  /**
   * 后继节点
   */
  next: Vertex;
}

/**
 * 有向无环图
 */
export interface Graph {
  /**
   * 图的节点数组
   */
  nodes: Vertex[];
  /**
   * 图的节点的个数
   */
  get count(): number;
}

以下则是基于上述的结构实现的拓扑排序：

/**
 * 拓扑排序
 */
export function topologicalSort(g: Graph) {
  // 用于记住入度数
  const inDegreeMap: Map<Vertex, number> = new Map();
  // 队列，用于处理入度是0的点
  const queue: Vertex[] = [];
  const topSortResults: Vertex[] = [];
  let count = 0;
  // 初始化的时候，用map记住每个节点的入度数
  g.nodes.forEach((v) => {
    if (v.inDegree.length === 0) {
      queue.push(v);
    } else {
      inDegreeMap.set(v, v.inDegree.length);
    }
  });
  // 开始进行拓扑排序
  while (queue.length) {
    // 出队一个节点进行处理
    const vertex = queue.shift()!;
    // 将其加入到结果里面去
    topSortResults.push(vertex);
    // 处理的个数加1
    count++;
    // 处理出度
    vertex.outDegree.forEach((edge) => {
      const nextVertex = edge.next;
      // 获取后继节点的入度
      const inDegree = inDegreeMap.get(nextVertex)!;
      // 设置节点新的入度
      inDegreeMap.set(nextVertex, inDegree - 1);
      // 如果除开这个节点的话，下个节点的入度将会是0，说明经过这个操作之后它已经没有入度了，可以进行操作了
      if (inDegree === 1) {
        queue.push(nextVertex);
      }
    });
  }
  // 如果把所有的入度为0的节点都找过了，凡是发现不够总的节点个数，于是可以得出一个结论，某些节点的入度无论如何不可能是0，于是可以推导出图中存在回路的结论。
  if (count < g.count) {
    throw new Error("图中存在回路，无法进行拓扑排序~");
  }

  return topSortResults;
}

拓扑排序的应用之——课程选修

假设某大学的计算机专业学生的培养计划如下：

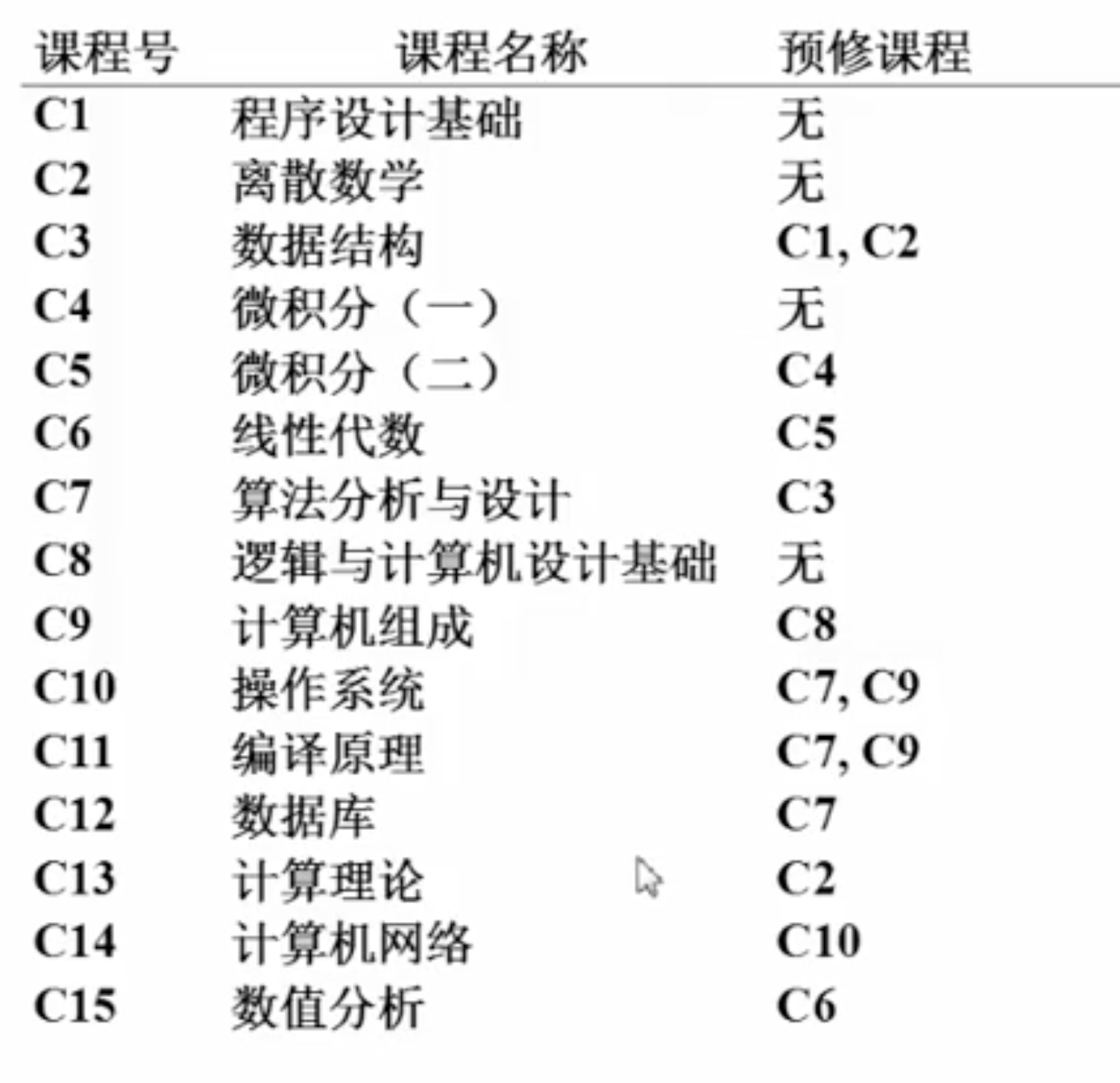
请输出其对应的排课顺序。

对于这个问题，我们采取上文所述的方式表达图。

我们用一个 json 来描述这个培养方案：

[
  {
    "name": "程序设计基础",
    "id": "c1",
    "deps": ""
  },
  {
    "name": "离散数学",
    "id": "c2",
    "deps": ""
  },
  {
    "name": "数据结构",
    "id": "c3",
    "deps": "c1,c2"
  },
  {
    "name": "微积分（上）",
    "id": "c4",
    "deps": ""
  },
  {
    "name": "微积分（下）",
    "id": "c5",
    "deps": "c4"
  },
  {
    "name": "线性代数",
    "id": "c6",
    "deps": "c5"
  },
  {
    "name": "算法分析与设计",
    "id": "c7",
    "deps": "c3"
  },
  {
    "name": "逻辑与计算机设计基础",
    "id": "c8",
    "deps": ""
  },
  {
    "name": "计算机组成",
    "id": "c9",
    "deps": "c8"
  },
  {
    "name": "操作系统",
    "id": "c10",
    "deps": "c7,c9"
  },
  {
    "name": "编译原理",
    "id": "c11",
    "deps": "c7,c9"
  },
  {
    "name": "数据库",
    "id": "c12",
    "deps": "c7"
  },
  {
    "name": "计算理论",
    "id": "c13",
    "deps": "c2"
  },
  {
    "name": "计算机网络",
    "id": "c14",
    "deps": "c10"
  },
  {
    "name": "数值分析",
    "id": "c15",
    "deps": "c6"
  }
]

id 为每个课程的唯一性标识，name 为课程的名称，deps 为课程的前置课程，多门课程以逗号分隔。

首先需要得到一个DAG，因此我们需要对这个 json 进行加工，以下是根据 json 生成DAG的算法：

export class BuildDAG {
  /**
   * 用于存储课程的信息映射
   */
  private refMap: Map<string, VertexInfo> = new Map();
  /**
   * 用于存储已经构建好的节点，防止重复构建
   */
  private builtMap: Map<string, Vertex> = new Map();
  /**
   * 存储外界传递的课程信息
   */
  private vertexInfo: VertexInfo[];

  constructor(vertexInfo: VertexInfo[]) {
    this.vertexInfo = vertexInfo;
  }

  /**
   * 链接两个节点
   * @param startVertex 开始节点
   * @param endVertex 结束节点
   */
  private link(startVertex: Vertex, endVertex: Vertex): void {
    const edge: Edge = {
      prev: startVertex,
      next: endVertex,
    };
    startVertex.outDegree.push(edge);
    endVertex.inDegree.push(edge);
  }
  /**
   * 构建顶点
   * @param name 顶点的名称
   * @param deps 顶点的依赖节点
   */
  private buildVertex(id: string) {
    const vertexInfo = this.refMap.get(id);
    // 找不到节点
    if (!vertexInfo) {
      return null;
    }
    // 如果节点已经被构建，可以直接返回已经构建的节点
    if (this.builtMap.get(id)) {
      return this.builtMap.get(id);
    }
    const { id: vertexId, deps, name } = vertexInfo;
    // 初始化节点信息
    const vertex: Vertex = {
      name,
      inDegree: [],
      outDegree: [],
    };
    // 递归的构建当前节点的前驱节点，若有的话
    const depsNodes: Vertex[] =
      deps === ""
        ? []
        : deps.split(",").map((depId) => {
            return this.buildVertex(depId) as Vertex;
          });
    // 将有依赖关系的节点建立关系
    depsNodes.forEach((pre) => {
      this.link(pre, vertex);
    });
    // 将当前已经构建的节点加入到已构建的哈希表中
    this.builtMap.set(vertexId, vertex);
    return vertex;
  }

  /**
   * 构建图
   */
  private buildGraph(): Graph {
    // 跟姐ID建立节点的映射关系
    this.vertexInfo.forEach((item) => {
      this.refMap.set(item.id, item);
    });
    // 依次构建每个节点
    const nodes = this.vertexInfo.map((v) => {
      return this.buildVertex(v.id) as Vertex;
    });
    return {
      nodes,
      get count() {
        return nodes.length;
      },
    };
  }

  build() {
    return this.buildGraph();
  }
}

对这个图进行拓扑排序得到的结果：

[
  "程序设计基础",
  "离散数学",
  "微积分（上）",
  "逻辑与计算机设计基础",
  "数据结构",
  "计算理论",
  "微积分（下）",
  "计算机组成",
  "算法分析与设计",
  "线性代数",
  "操作系统",
  "编译原理",
  "数据库",
  "数值分析",
  "计算机网络"
]

有了这个结果，那么我们就可以直接根据每个学期学生需要完成的课程数进行分块，每块就是该学生对应学期需要完成的课程。

拓扑排序的应用之——Monorepo项目的构建顺序

现在的开源库已经逐渐采用pnpm+Monorepo的管理方式，其拥有以下优点：

• 代码共享和重用： 在Monorepo中，不同部分的代码可以轻松共享和重用。这有助于避免重复工作，提高代码的一致性，并使开发人员更容易找到和使用已经存在的功能模块或库。

• 统一的构建和部署： 由于所有代码都在一个仓库中，构建和部署过程变得更加统一和协调。这有助于确保不同部分的代码之间没有不兼容性，减少构建和部署的问题。

• 版本一致性： 在Monorepo中，所有代码都可以使用相同的版本控制系统和工具进行管理。这有助于确保项目的各个部分保持一致的版本，减少版本冲突和依赖问题。

• 易于跟踪更改： Monorepo使得跟踪项目中的更改变得更加容易，因为所有更改都在同一个仓库中进行。这有助于开发团队更好地理解和管理代码变更。

• 简化协作： 当多个团队或开发者同时工作在一个项目中时，Monorepo可以简化协作过程。开发者可以更容易地查看和理解整个项目的状态，而不必在不同的仓库之间切换。

• 提高构建性能： 在一些情况下，Monorepo可以提高构建性能。因为代码和依赖项都在一个仓库中，可以更有效地利用缓存和并行构建，从而加快构建时间。

• 强化代码质量控制： 通过将所有代码集中在一个仓库中，可以更容易地实施代码审查、测试和代码质量控制标准，确保高质量的代码交付。

虽然Monorepo模式拥有以上优点，但是Monorepo模式自然就逃不过一个问题——>依赖的先后顺序问题。

假设 B 项目依赖 A 项目，若 A 项目没有构建成功，B 项目是肯定不会构建成功的，因此，我们就需要得到一个科学的构建关系，怎么样得到这个科学的构建关系，即对依赖关系进行拓扑排序。

以下是我所在公司一个基于Monorepo模式管理的项目的依赖关系：

[
  {
    "id": "@funny/widgets",
    "deps": ["@funny/env"]
  },
  {
    "id": "@funny/track",
    "deps": ["@funny/env"]
  },
  {
    "id": "@funny/share",
    "deps": [
      "@funny/env",
      "@funny/bridge",
      "@funny/cross-platform",
      "@funny/goto",
      "@funny/request",
      "@funny/widgets"
    ]
  },
  {
    "id": "@funny/env",
    "deps": []
  },
  {
    "id": "@funny/goto",
    "deps": [
      "@funny/env",
      "@funny/bridge",
      "@funny/cross-platform",
      "@funny/request",
      "@funny/track",
      "@funny/widgets"
    ]
  },
  {
    "id": "@funny/request",
    "deps": ["@funny/env"]
  },
  {
    "id": "@funny/core",
    "deps": [
      "@funny/env",
      "@funny/bridge",
      "@funny/cross-platform",
      "@funny/goto",
      "@funny/request",
      "@funny/share",
      "@funny/track",
      "@funny/widgets"
    ]
  },
  {
    "id": "@funny/bridge",
    "deps": ["@funny/env", "@funny/cross-platform"]
  },
  {
    "id": "@funny/cross-platform",
    "deps": ["@funny/env", "@funny/widgets"]
  }
]

经过拓扑排序之后，得到的科学的依赖构建顺序如下：

[
  "@funny/env",
  "@funny/widgets",
  "@funny/track",
  "@funny/request",
  "@funny/cross-platform",
  "@funny/bridge",
  "@funny/goto",
  "@funny/share",
  "@funny/core"
]

因为 deps 改成了数组，只需要简单的调整上述算法即可，因此此处不再赘述。