最短路径

最短路径问题，这个问题几乎是我们每天必定会接触到的问题了吧。

当你打开高德地图，输入目的地，高德地图一下就可以给你计算出来了怎么走，甚至还能让你选条件，比如途经点，用时最短，里程最短等条件。我一直感叹其中的神奇，在我没有接触图这章的知识的时候，想破脑袋也不知道其中的原理，但是我从未放弃过要去搞明白计算机是怎么样解决这类问题的。

曾经我有一个朋友，他是银行职员，当时正值炎炎夏日，他需要在一周内拜访成都市区几百家客户，他来求助我，是否可以帮忙写一个程序算一下怎么安排这些客户的拜访顺序，囿于当时我的水平有限，只能遗憾的告诉他我不会啊，真实心疼他。他的这个需求其实是结合了图的最短路径问题和最小生成树问题的场景。

如果你掌握了本节内容，将来和朋友们出去玩儿的时候，编程求解旅行的规划，那应该可以狠狠地秀大家一把吧；

如果你不仅掌握了本节内容，还掌握了后面将会介绍的最小生成树问题，将来某一天大家有类似我朋友这种极端的需求的时候，一定可以帮到他哟，这就是程序员的力量，代码的魅力，加油，拿下这节知识。

无权图单源最短路

无权图的单源最短路问题，跟我们的广度优先遍历的思路非常相似，我们从起点出发，依次操作当前节点的邻接点，若其还没有处理过，则处理，并且更新起点到这个点的距离，然后还要把这个点加到我们记录的一个路径数据集里面去。重复上述操作，直到处理完图中所有的点。

我们以这个图为例：

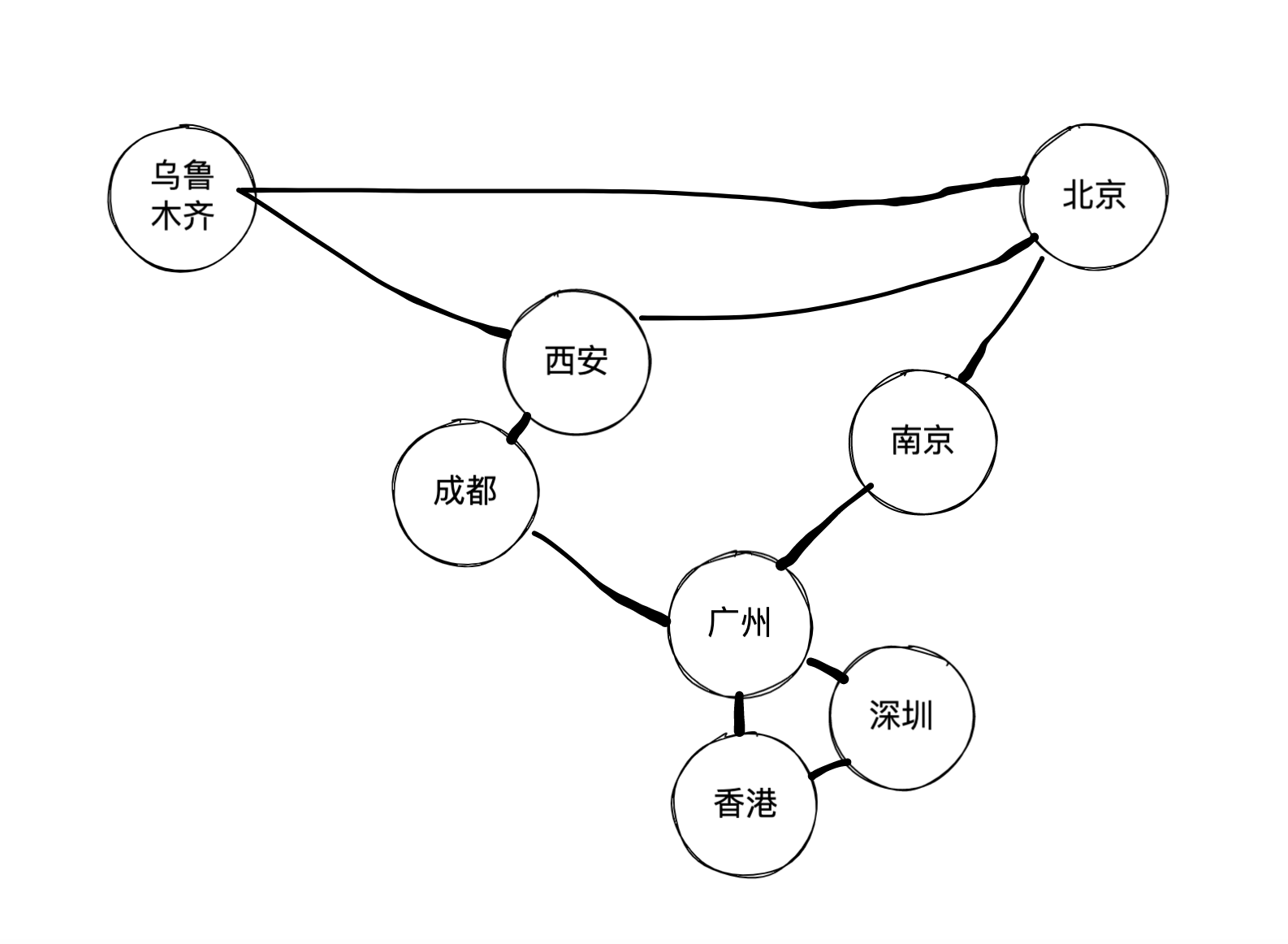
并且以如下表示方法表示图：

/**
 * 边类
 */
class Edge {
  constructor(name) {
    this.name = name;
  }
  /**
   * 边的编号
   */
  name;
  /**
   * 起始点
   * @type {Vertex}
   */
  from;
  /**
   * 终止点
   * @type {Vertex}
   */
  to;
}

/**
 * 顶点类
 */
class Vertex {
  /**
   * 城市名称
   */
  cityName;
  /**
   * 邻接点
   */
  siblings = [];
  constructor(cityName) {
    this.cityName = cityName;
  }
}

/**
 * 图类
 */
class Graph {
  /**
   * 顶点集合
   * @type {Vertex[]}
   */
  vertexList = [];
  /**
   * 边集合
   * @type {Edge[]}
   */
  edgeList = [];
  /**
   * 向图中插入一个顶点
   */
  addVertex(v) {
    this.vertexList.push(v);
  }
  /**
   * 增加边，连接from和to两个顶点
   * @param {Vertex} from
   * @param {Vertex} to
   */
  addEdge(from, to) {
    const name = `${from.cityName}至${to.cityName}`;
    const edge = new Edge(name);
    this.edgeList.push(edge);
    from.siblings.push(to);
    to.siblings.push(from);
  }
}

接着，根据上面的那个图，构建出我们想要的连接关系：

const g = new Graph();
const beijing = new Vertex("北京");
const nanjing = new Vertex("南京");
const guangzhou = new Vertex("广州");
const shenzhen = new Vertex("深圳");
const hongkong = new Vertex("香港");
const chengdu = new Vertex("成都");
const xian = new Vertex("西安");
const urumchi = new Vertex("乌鲁木齐");
/**
 * 将城市加入到图中
 */
g.addVertex(beijing);
g.addVertex(nanjing);
g.addVertex(guangzhou);
g.addVertex(shenzhen);
g.addVertex(hongkong);
g.addVertex(chengdu);
g.addVertex(xian);
g.addVertex(urumchi);
/**
 * 建立连接关系
 */
g.addEdge(beijing, nanjing);
g.addEdge(beijing, xian);
g.addEdge(nanjing, guangzhou);
g.addEdge(guangzhou, shenzhen);
g.addEdge(guangzhou, hongkong);
g.addEdge(hongkong, shenzhen);
g.addEdge(chengdu, guangzhou);
g.addEdge(chengdu, xian);
g.addEdge(urumchi, xian);
g.addEdge(urumchi, beijing);

那么，最短路径求解算法如下：

/**
 * 单源无权图的最短路算法
 * @param {Vertex} start
 * @param {Vertex} end
 */
function unweightedShortestPath(start, end) {
  const queue = [];
  /* 距离哈希表，用于存储开始顶点到任意节点的距离 */
  const dist = new Map();
  /* 路径哈希表，用于存储开始顶点到任意节点所经过的顶点 */
  const path = new Map();
  dist.set(start, 0);
  queue.push(start);
  while (queue.length > 0) {
    let vertex = queue.shift();
    for (let i = 0; i < vertex.siblings.length; i++) {
      // 取出当前正在处理的顶点的邻接点进行处理
      let adjoinVertex = vertex.siblings[i];
      /* 若adjoinVertex未被访问过 */
      if (typeof dist.get(adjoinVertex) === "undefined") {
        /* 将这个点到start的距离更新 */
        dist.set(adjoinVertex, dist.get(vertex) + 1);
        /* 将这个点记录在S到adjoinVertex的路径上 */
        path.set(adjoinVertex, vertex);
        // 并且将当前邻接点入队
        queue.push(adjoinVertex);
      }
    }
  }
  // 获取终点的最短路径长度
  const distance = dist.get(end);
  // 使用栈记住终点
  const stack = [end];
  let preVertex = path.get(end);
  // 沿途处理从终点到起点所经过的路径
  while (preVertex) {
    stack.push(preVertex);
    // 继续向上迭代，寻找经过的顶点
    preVertex = path.get(preVertex);
  }
  // 经过逆序，得到了正确的路径
  let via = "";
  while (stack.length) {
    const city = stack.pop();
    via += "->" + city.cityName;
  }
  return { distance, path: via.replace(/(^->)|(->$)/g, "") };
}

假设我们想求出成都到北京的最短距离，并且需要求出是怎么样达到北京的，如下：

const { path, distance } = unweightedShortestPath(chengdu, beijing);
// path 成都->西安->北京
// distance 3

下面，我们画图描述一下这个处理流程。

首先，在开始时将成都入队，同时设置距离为0，因为我们设置了它的距离，其实际上就相当于之前我们在广度优先遍历节的时候所提到的标记当前的节点已经被处理的手段，一举两得。接着，我们把成都出队，准备处理它的邻接点。

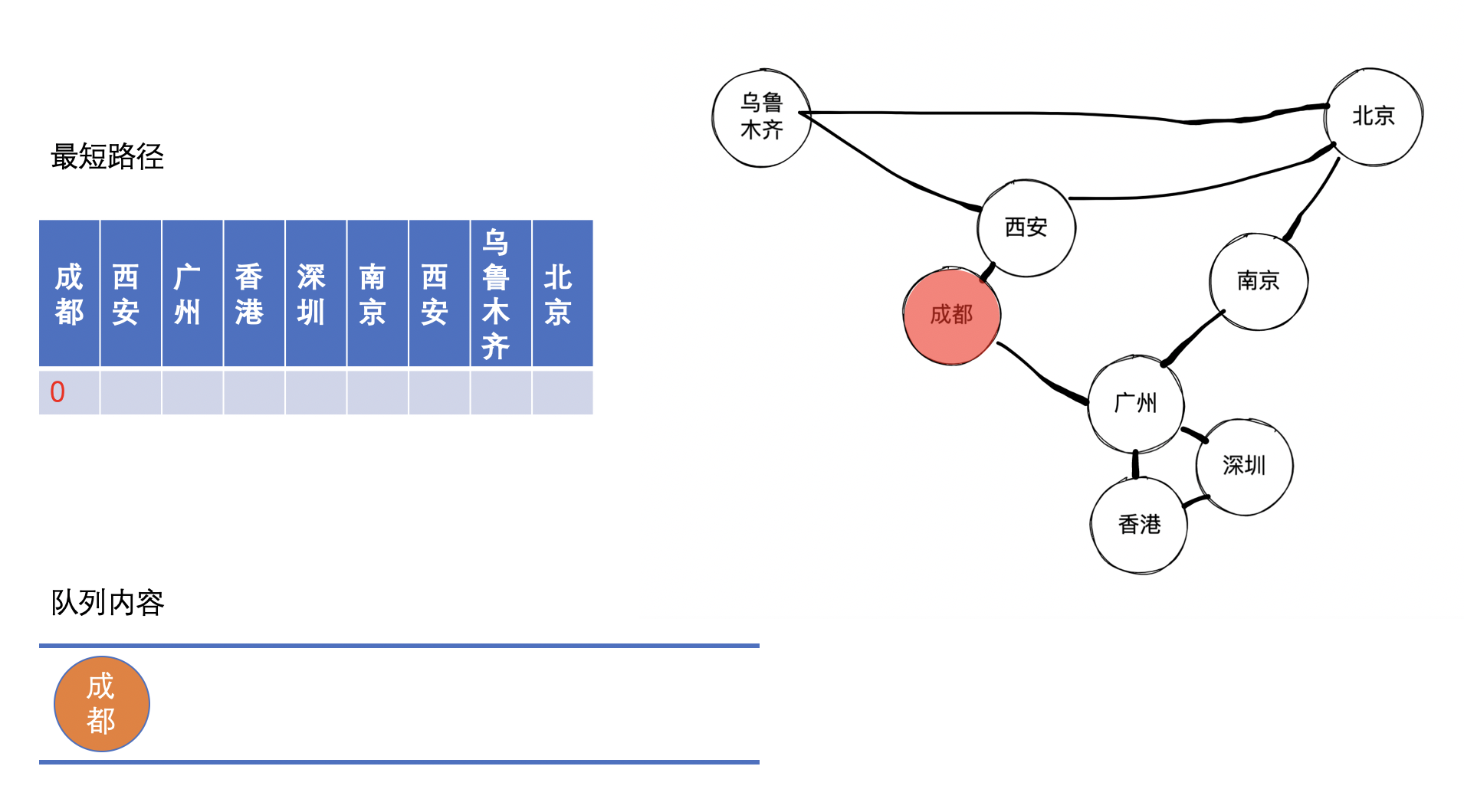
紧接着，我们把西安和广州入队

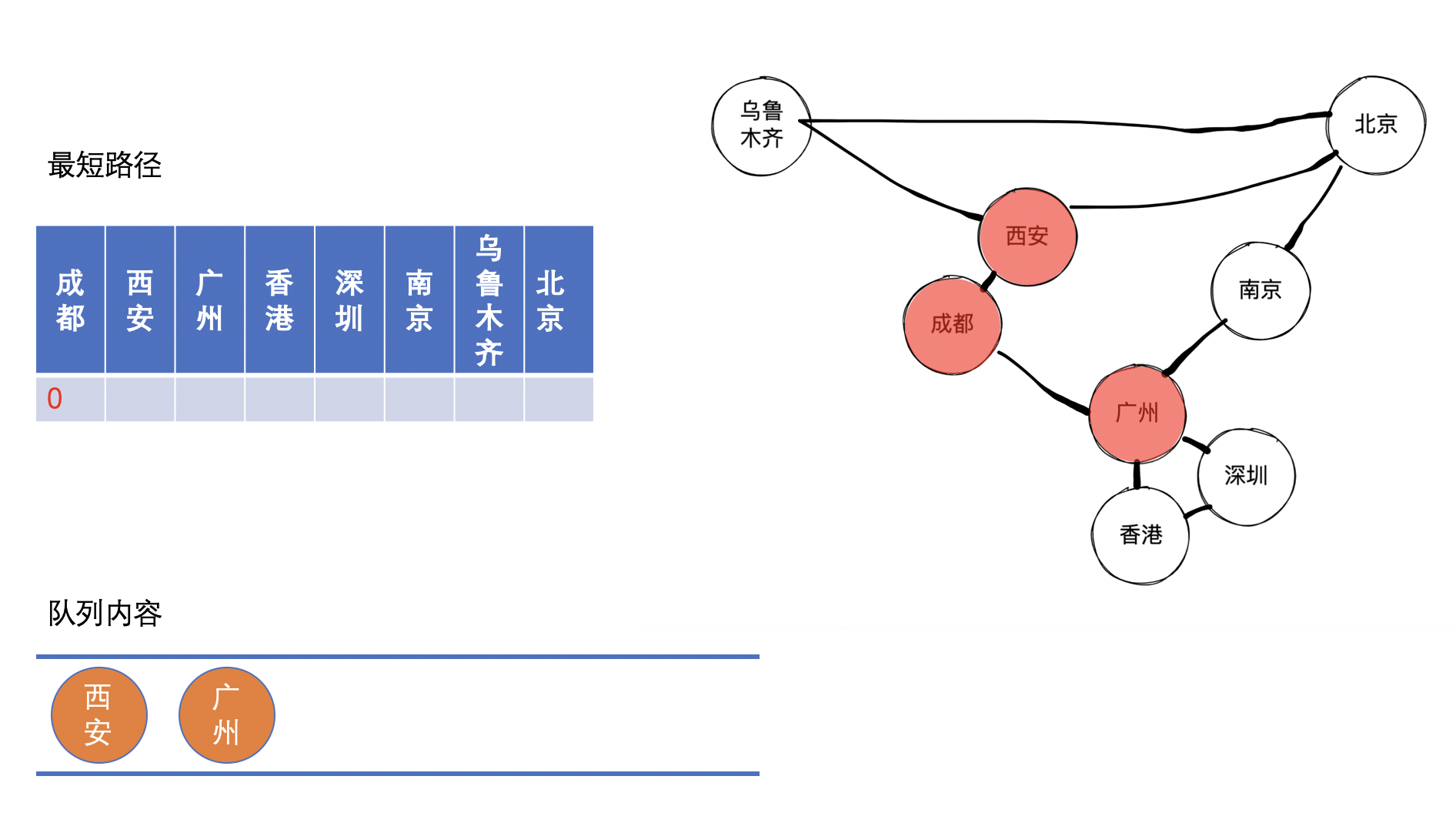
接着，把西安出队，同时标记成都到西安的最短距离，然后将西安的邻接节点乌鲁木齐和北京入队。

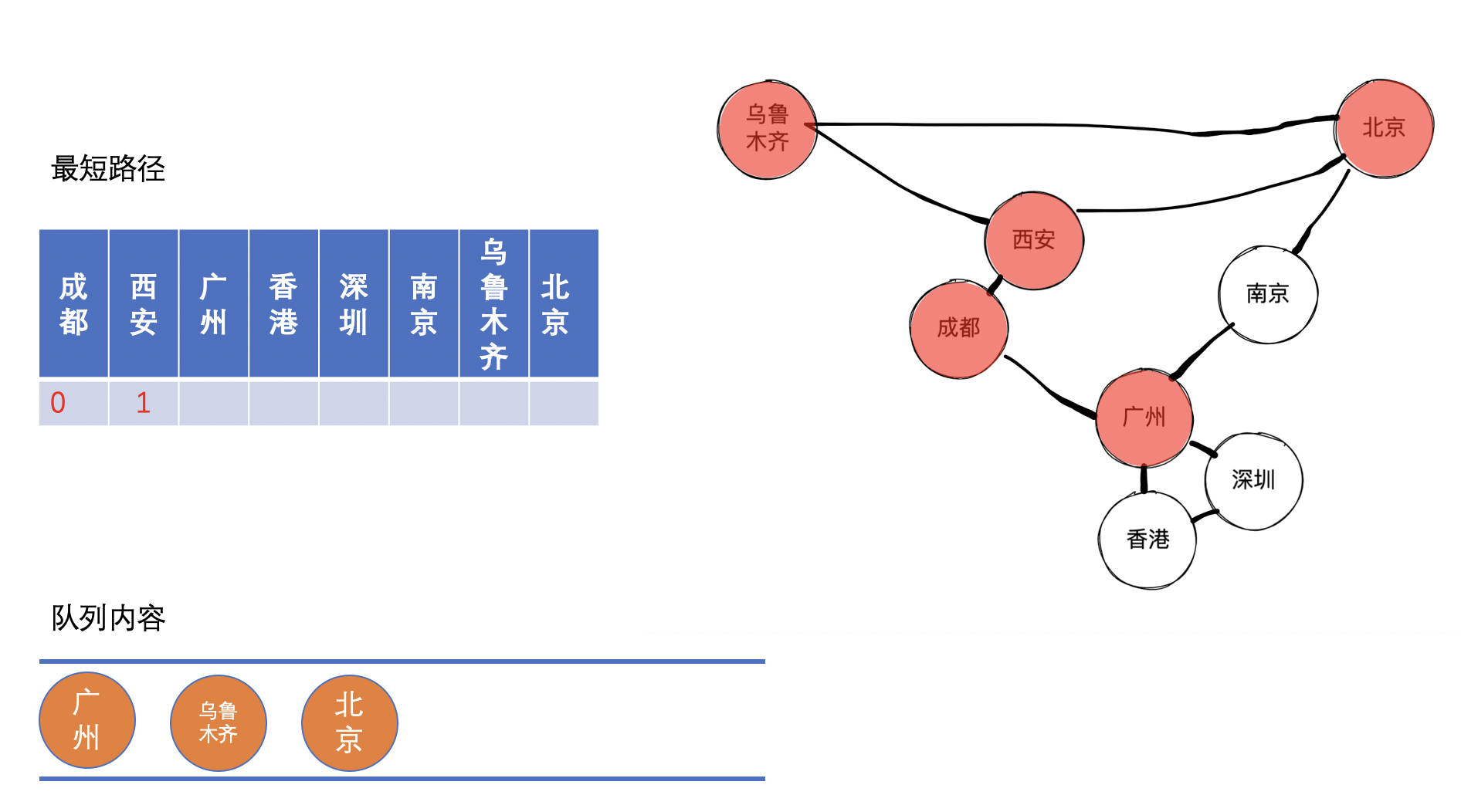
接着，把广州出队，同时标记成都到广州的最短距离，然后将广州的邻接节点深圳、香港和南京入队。

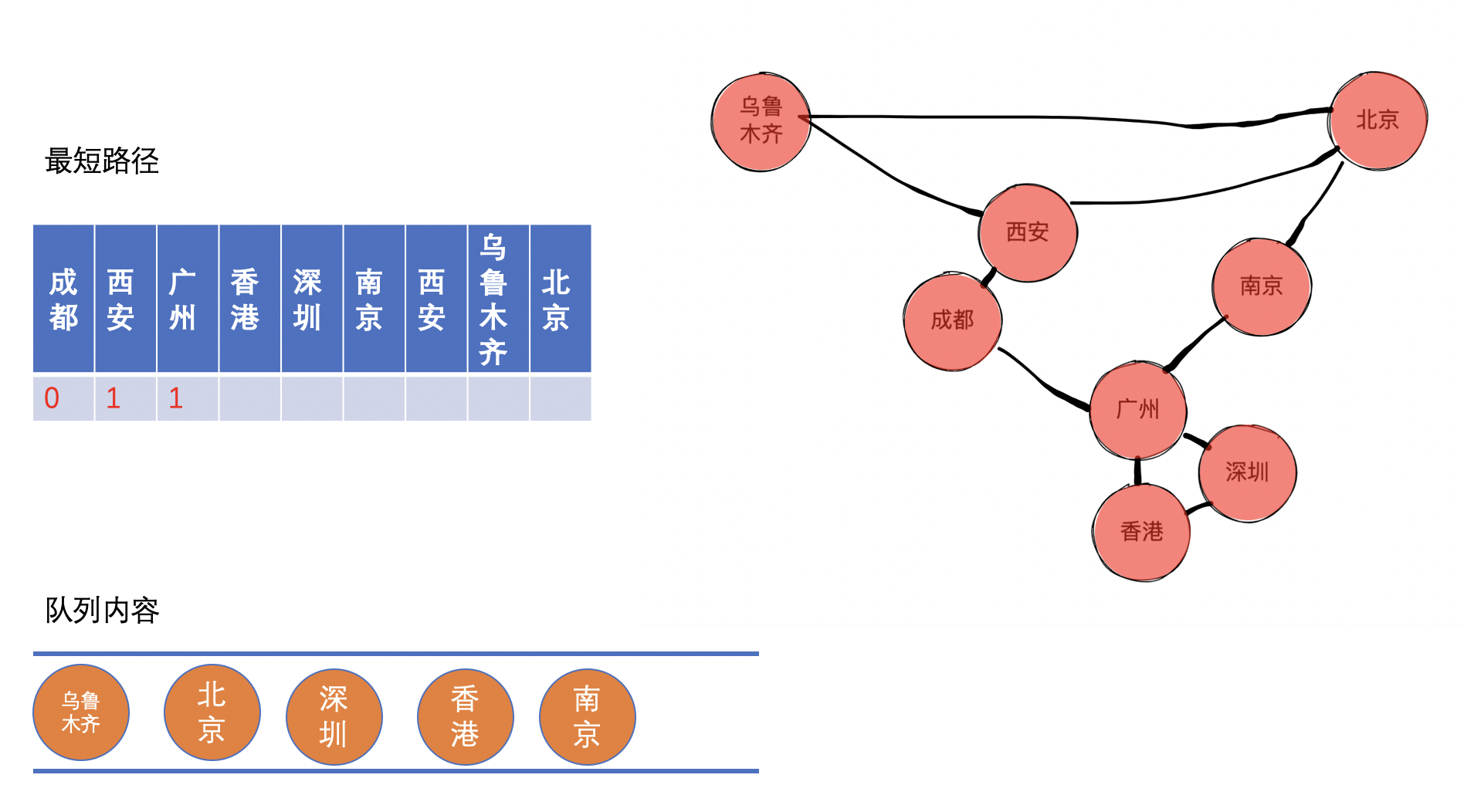
接着，把乌鲁木齐出队，同时标记成都到乌鲁木齐的最短距离，然后把乌鲁木齐的邻接节点加入队列（虽然会将其邻接点加入队列，但是因为后面其实这些邻接点并不会重复处理，为了简便起见，我们在图上就不体现其邻接节点加入队列的过程）。

乌鲁木齐到成都需要经过西安，已知成都到西安的距离，故可以求得成都到乌鲁木齐的距离。

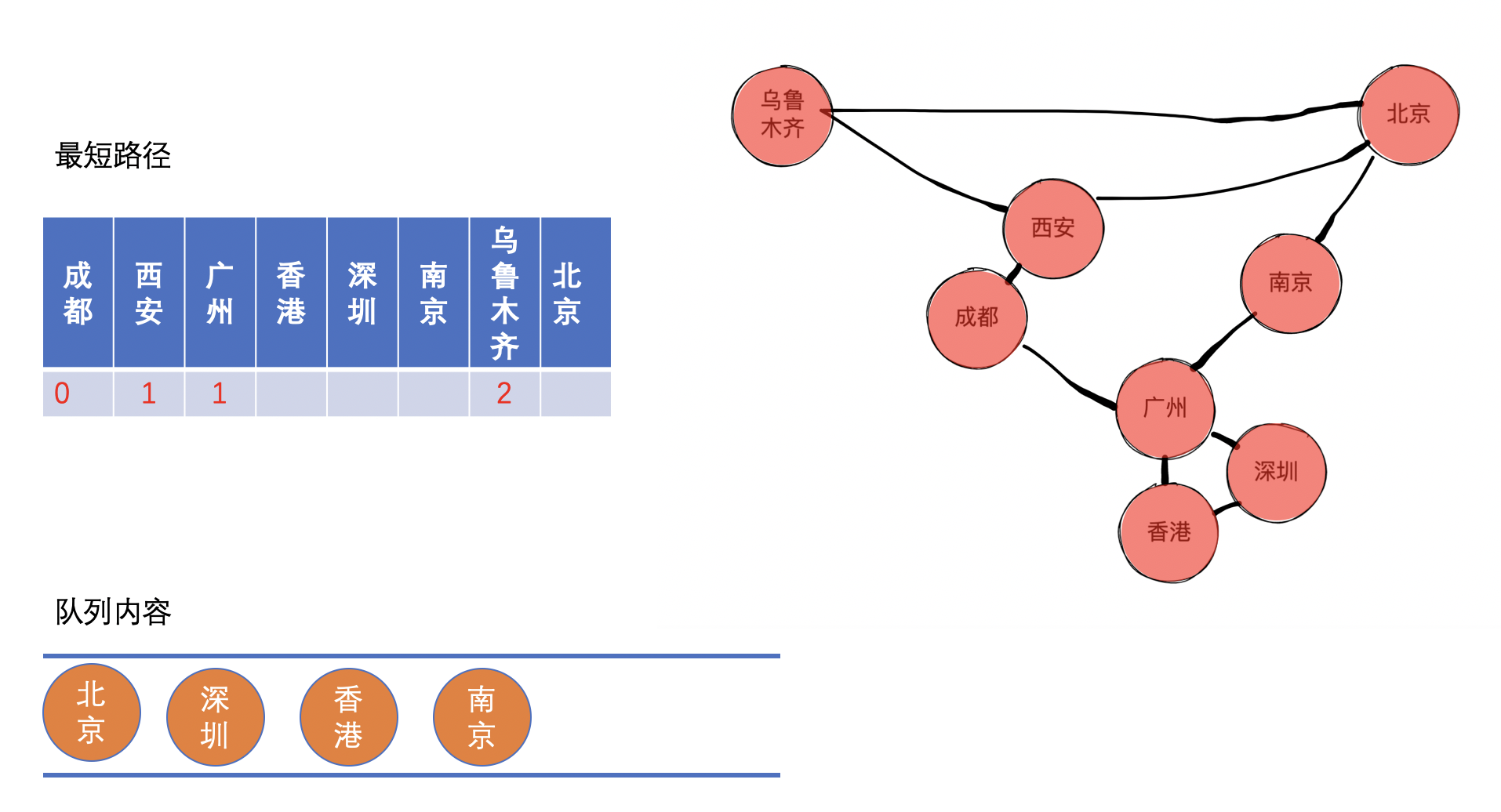
接着，把北京出队，同时标记成都到北京的最短距离，然后把北京的邻接节点加入队列，同理，邻接节点入队这个过程我们图上就没有体现了。

北京到成都需要经过西安，已知成都到西安的距离，故可以求得成都到北京的距离。

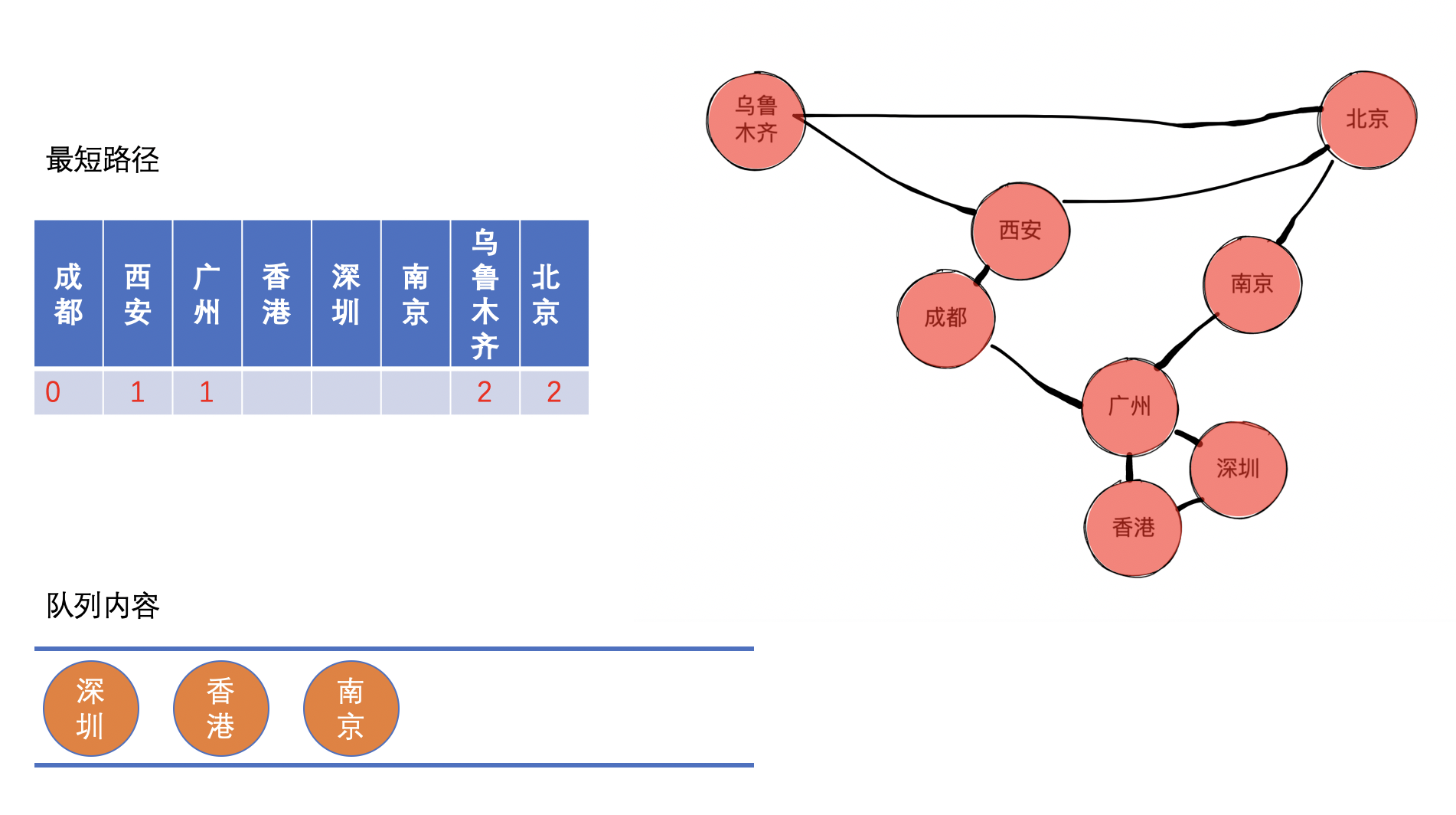
同理可以求得深圳、香港、南京的最短距离。

即最终结果如下：

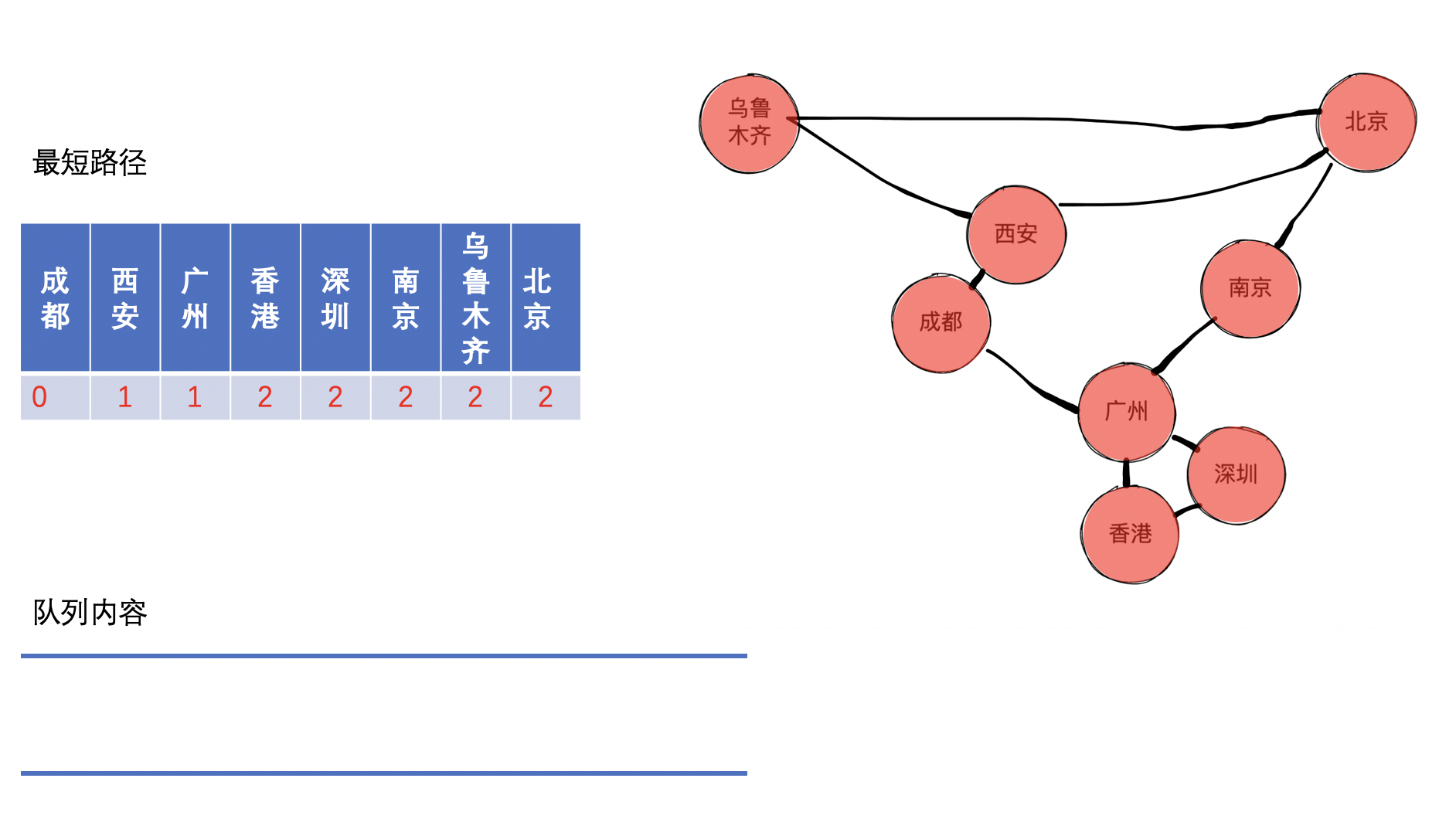
因为我们在求解过程中把经过的路径已经计算出来了，类同于链表的原理，我们可以从终点倒推到起点，便可以求得经过的节点，因为这个是一个逆序的结果，所以我们需要使用栈再次将其逆序，即可求得最终的结果。

不管是有向还是无向图，我们都可以使用上述算法求得从某个指定的开始节点到所有节点的最短路径。

带权图单源最短路径算法

对于这个问题，我们还是基于上面我们使用的那个城市相对位置的例子来阐述，不过，需要引入权重。

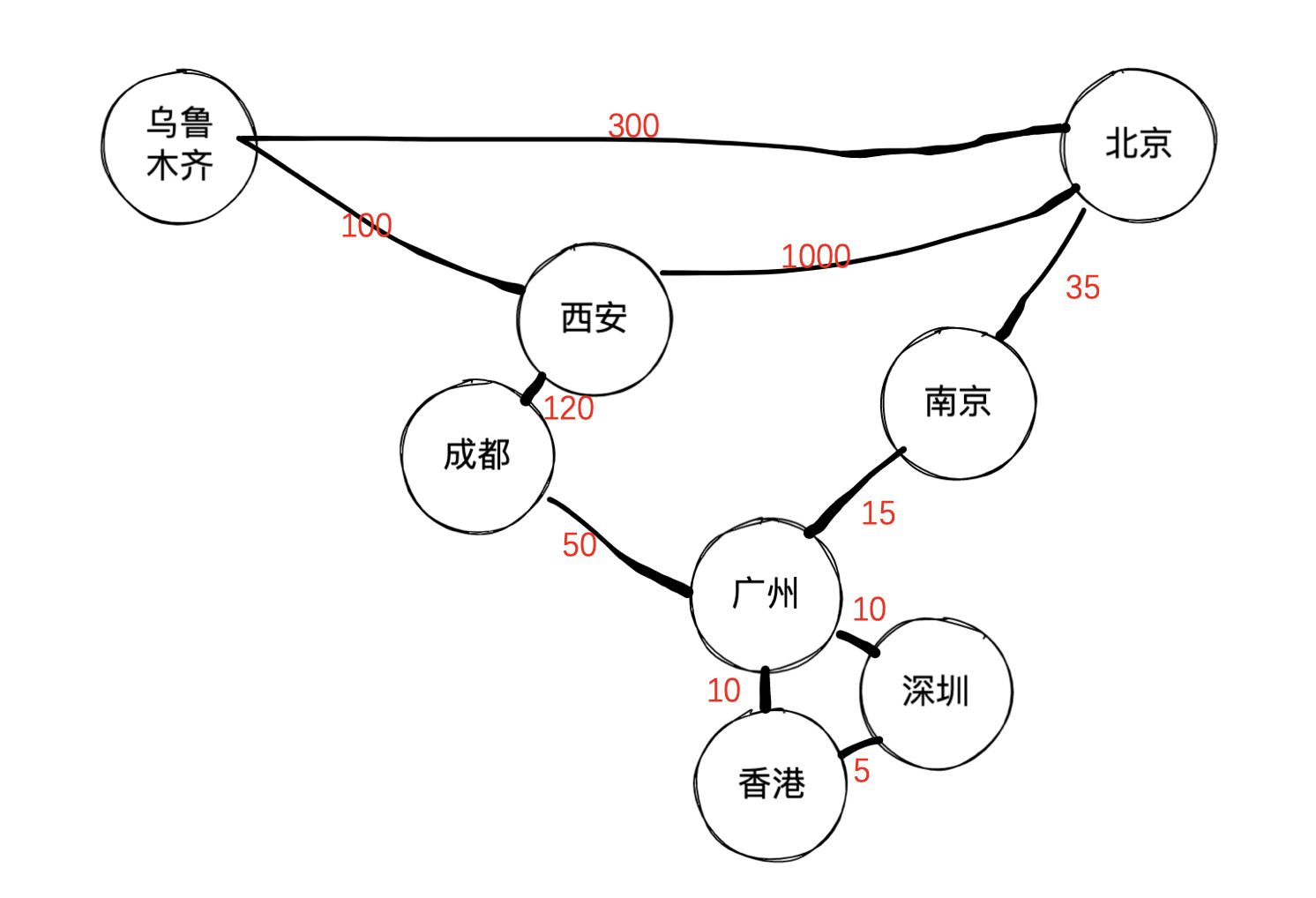
因为增加了权重，上面的表示方法也有一定的调整：

class Edge {
  constructor(name, cost) {
    this.name = name;
    this.cost = cost;
  }
  /**
   * 边的编号
   */
  name;
  /**
   * 起始点
   * @type {Vertex}
   */
  from;
  /**
   * 终止点
   * @type {Vertex}
   */
  to;
  /**
   * @type {number}
   */
  cost;
}

class Vertex {
  constructor(cityName) {
    this.cityName = cityName;
  }
  /**
   * 城市名称
   */
  cityName;
  /**
   * 邻接边
   */
  edges = [];
}

class Graph {
  /**
   * 顶点列表
   */
  vertexList = [];

  addVertex(v) {
    this.vertexList.push(v);
  }
  /**
   * 增加边
   * @param {Vertex} from
   * @param {Vertex} to
   * @param {number} cost
   */
  addEdge(from, to, cost) {
    const into = new Edge(`${from.cityName}至${to.cityName}`, cost);
    const outside = new Edge(`${to.cityName}至${from.cityName}`, cost);
    // 建立两个城市的指向关系
    from.edges.push(outside);
    to.edges.push(into);
  }
}

然后，初始化数据：

const g = new Graph();
const beijing = new Vertex("北京");
const nanjing = new Vertex("南京");
const guangzhou = new Vertex("广州");
const shenzhen = new Vertex("深圳");
const hongkong = new Vertex("香港");
const chengdu = new Vertex("成都");
const xian = new Vertex("西安");
const urumchi = new Vertex("乌鲁木齐");

/**
 * 将城市加入到图中
 */
g.addVertex(beijing);
g.addVertex(nanjing);
g.addVertex(guangzhou);
g.addVertex(shenzhen);
g.addVertex(hongkong);
g.addVertex(chengdu);
g.addVertex(xian);
g.addVertex(urumchi);
/**
 * 建立连接关系
 */
g.addEdge(beijing, nanjing, 35);
g.addEdge(beijing, xian, 1000);
g.addEdge(nanjing, guangzhou, 15);
g.addEdge(guangzhou, shenzhen, 10);
g.addEdge(guangzhou, hongkong, 10);
g.addEdge(hongkong, shenzhen, 10);
g.addEdge(chengdu, guangzhou, 50);
g.addEdge(chengdu, xian, 120);
g.addEdge(urumchi, xian, 100);
g.addEdge(urumchi, beijing, 300);

接下来是根据上面图的表示方法给出的对应求解的核心代码，也就是大名鼎鼎的迪杰斯特拉算法：

/**
 * 在图中返回未被收录顶点中dist最小者
 * @param {Graph} graph
 * @param {Map<number, number>} distance
 * @param {Map<Vertex, boolean>} collected
 * @returns {Vertex | null}
 */
function findMinDist(graph, distance, collected) {
  /* 返回未被收录顶点中dist最小顶点 */
  let minVertex;
  let minDist = Infinity;
  for (let i = 0; i < graph.vertexList.length; i++) {
    const curVertex = graph.vertexList[i];
    /* 若curVertex未被收录，且dist.get(curVertex)更小 */
    if (!collected.get(curVertex) && distance.get(curVertex) < minDist) {
      /* 更新最小距离 */
      minDist = distance.get(curVertex);
      /* 更新对应顶点 */
      minVertex = curVertex;
    }
  }
  // 如果能够找到这样的顶点，则返回最小的距离，否则，这样的距离不存在
  return minDist < Infinity ? minVertex : null;
}

/**
 * 迪杰斯特拉算法求解最短路径
 * @param {Graph} graph
 * @param {Vertex} start
 * @returns
 */
function dijkstra(graph, start) {
  let collected = new Map();
  let distance = new Map();
  let path = new Map();
  /* 先将起点收入集合 */
  distance.set(start, 0);
  collected.set(start, true);
  graph.vertexList.forEach((vertex) => {
    if (vertex === start) {
      // 对start节点本身除外
      return;
    }
    // 找到start节点的邻接点，如果当前节点存在出度指向起点，则证明当前节点是开始节点的邻接点
    const neighborEdge = vertex.edges.find((v) => v.to === start);
    // 若存在连接的话，则按权重初试化，否则初始化为无穷大
    if (neighborEdge) {
      distance.set(vertex, neighborEdge.cost);
      path.set(vertex, start);
    } else {
      distance.set(vertex, Infinity);
    }
  });
  while (true) {
    /* vertex为未被收录顶点中distance最小者 */
    let vertex = findMinDist(graph, distance, collected);
    /* 若这样的vertex不存在，流程结束 */
    if (!vertex) {
      break;
    }
    /* 收录vertex */
    collected.set(vertex, true);
    /* 遍历图中的每个顶点 */
    for (let i = 0; i < graph.vertexList.length; i++) {
      let curVertex = graph.vertexList[i];
      /* 若curVertex是vertex的邻接点并且未被收录 */
      const linkEdge = curVertex.edges.find((edge) => edge.to === vertex);
      if (!collected.get(curVertex) && linkEdge) {
        /* 若有负边 */
        if (linkEdge < 0) {
          /* 不能正确解决，返回错误标记 */
          return { distance: null, path: null };
        }
        /* 若收录vertex使得distance变小 */
        if (distance.get(vertex) + linkEdge.cost < distance.get(curVertex)) {
          /* 更新dist */
          distance.set(curVertex, distance.get(vertex) + linkEdge.cost);
          /* 更新start到curVertex的路径 */
          path.set(curVertex, vertex);
        }
      }
    }
  }
  return { distance, path };
}

/**
 * 根据迪杰斯特拉算法求解结果求最终的结果
 * @param {Map<Vertex, number>} distance
 * @param {Map<Vertex, Vertex>} path
 * @param {Vertex} destination
 */
function getShortestPath(path, distance, destination) {
  if (path === null || distance === null) {
    return { cost: -1, path: null };
  }
  const stack = [destination];
  let preVertex = path.get(destination);
  while (preVertex) {
    stack.push(preVertex);
    preVertex = path.get(preVertex);
  }
  let via = "";
  let cost = distance.get(destination);
  while (stack.length) {
    via += "->" + stack.pop().cityName;
  }
  return { path: via.replace(/(^->)|(->$)/g, ""), cost };
}

我们来分析一下迪杰斯特拉算法的求解过程：

首先，将起始节点收录，然后找到它的所有邻接点，如果找的到邻接点的话，初始化该邻接点到起点的距离，并且将该邻接点更新在起始节点的路径上，西安和广州是成都的邻接点，因此可以得到如下图：

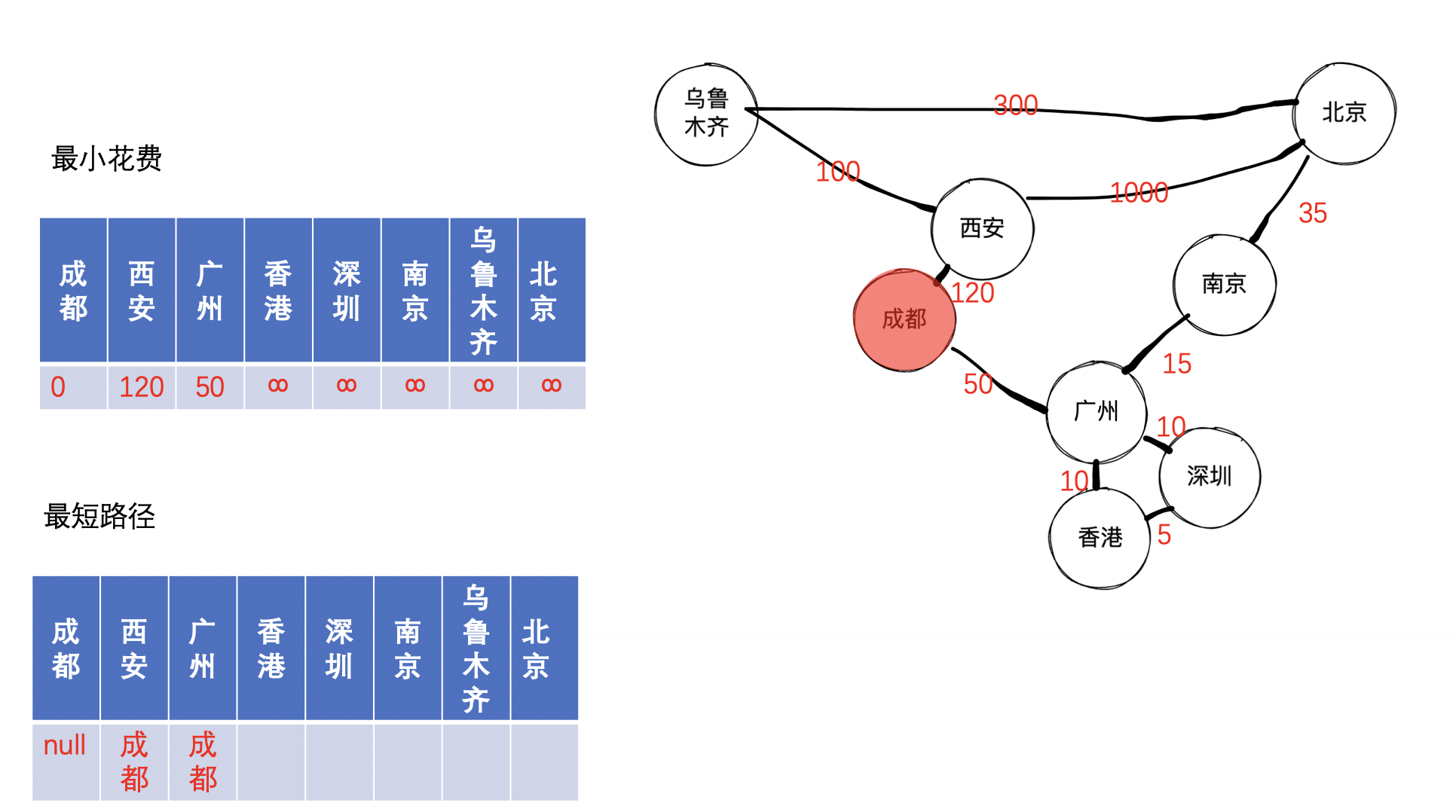
接着，我们找到未收录节点中的最小的节点，经过查找，找到的是广州，因为发现成都到南京，香港，深圳的距离由原来的无穷大变成经过广州再到对应的城市，因此可以更新距离和路径，可以得到如下图：

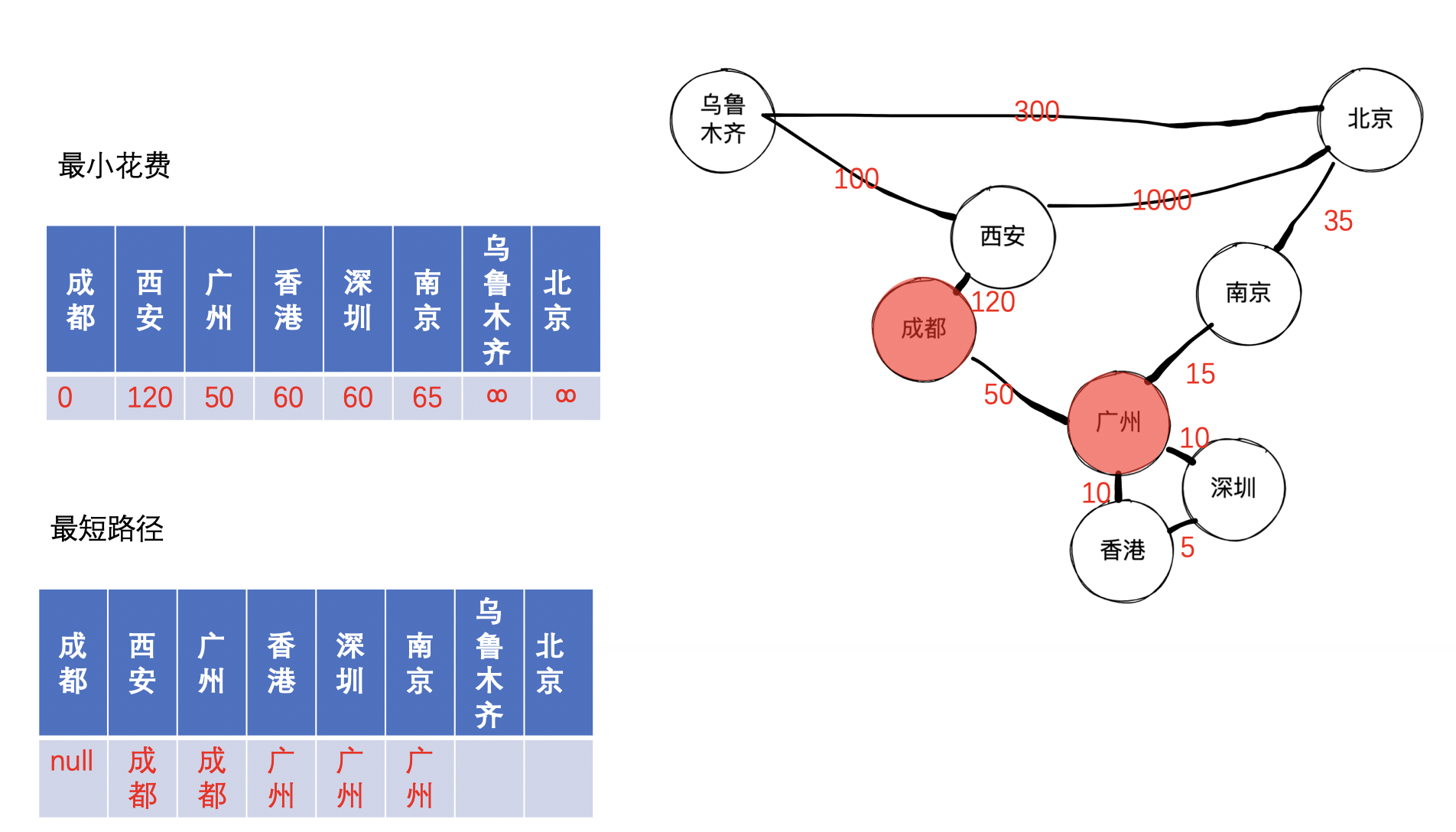
接着，继续找到未收录节点中的最小节点，经过查找，找到的是香港，因为发现成都到香港的距离可以保持不变，其邻接点深圳也是处理过的，因此，仅仅需要将香港收录，可以得到下图：

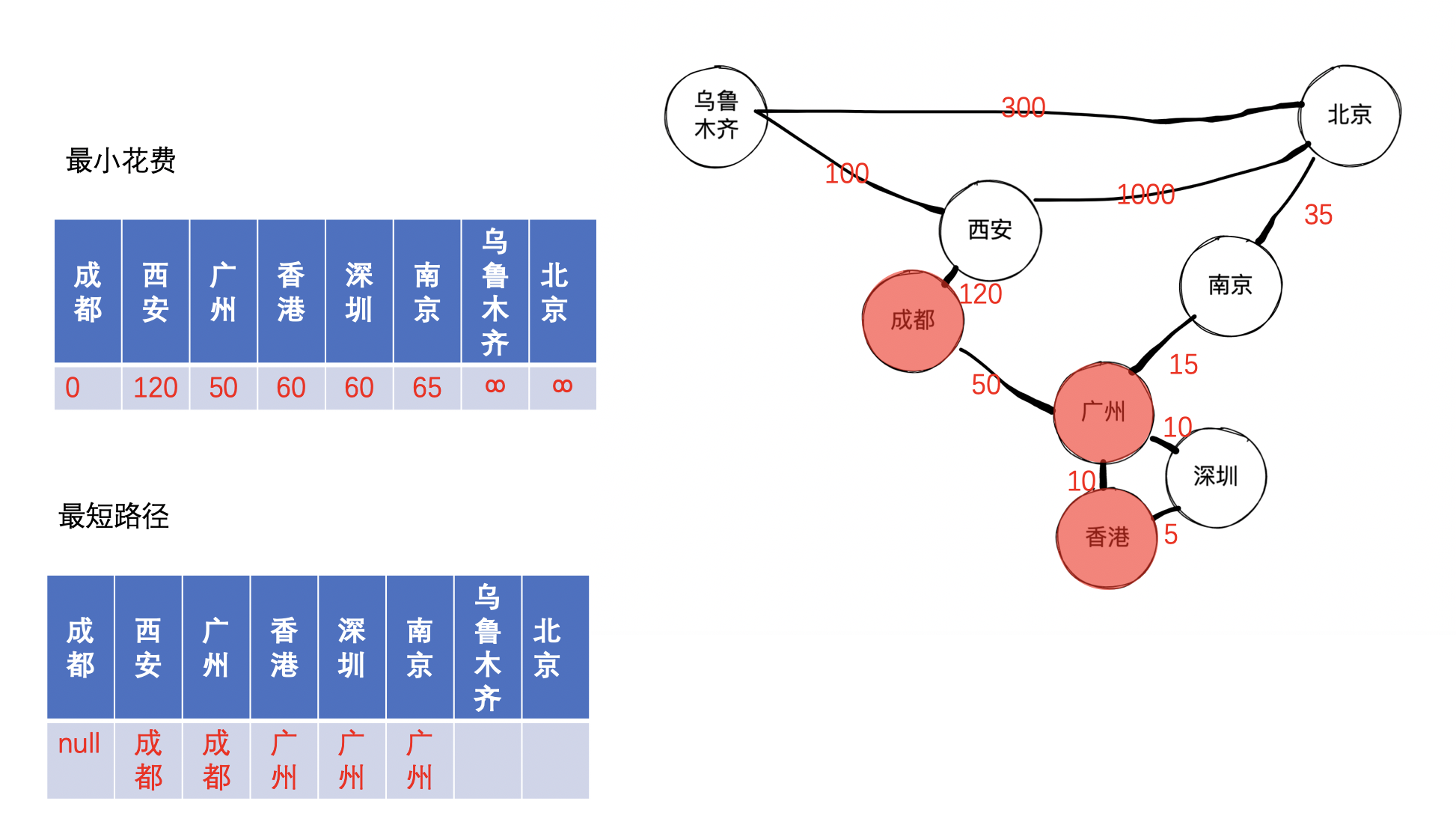
接着，继续找到未收录节点中的最小节点，经过查找，找到的是深圳，和香港同理，因此可以得到下图：

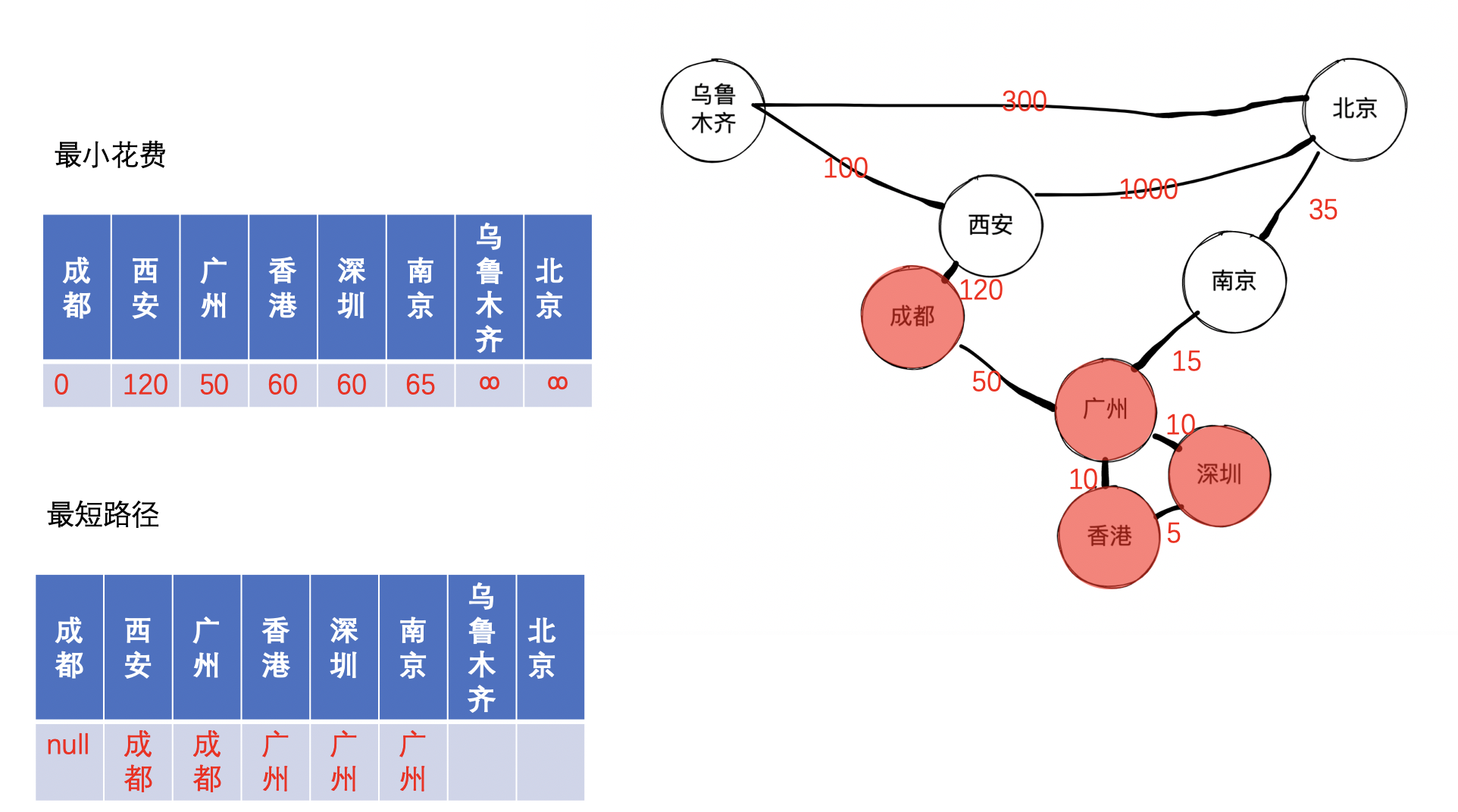
接着，我们找到未收录节点中的最小的节点，经过查找，找到的是南京，因为发现成都到北京的距离由原来的无穷大变成经过南京再到北京，因此可以更新距离和路径，可以得到如下图：

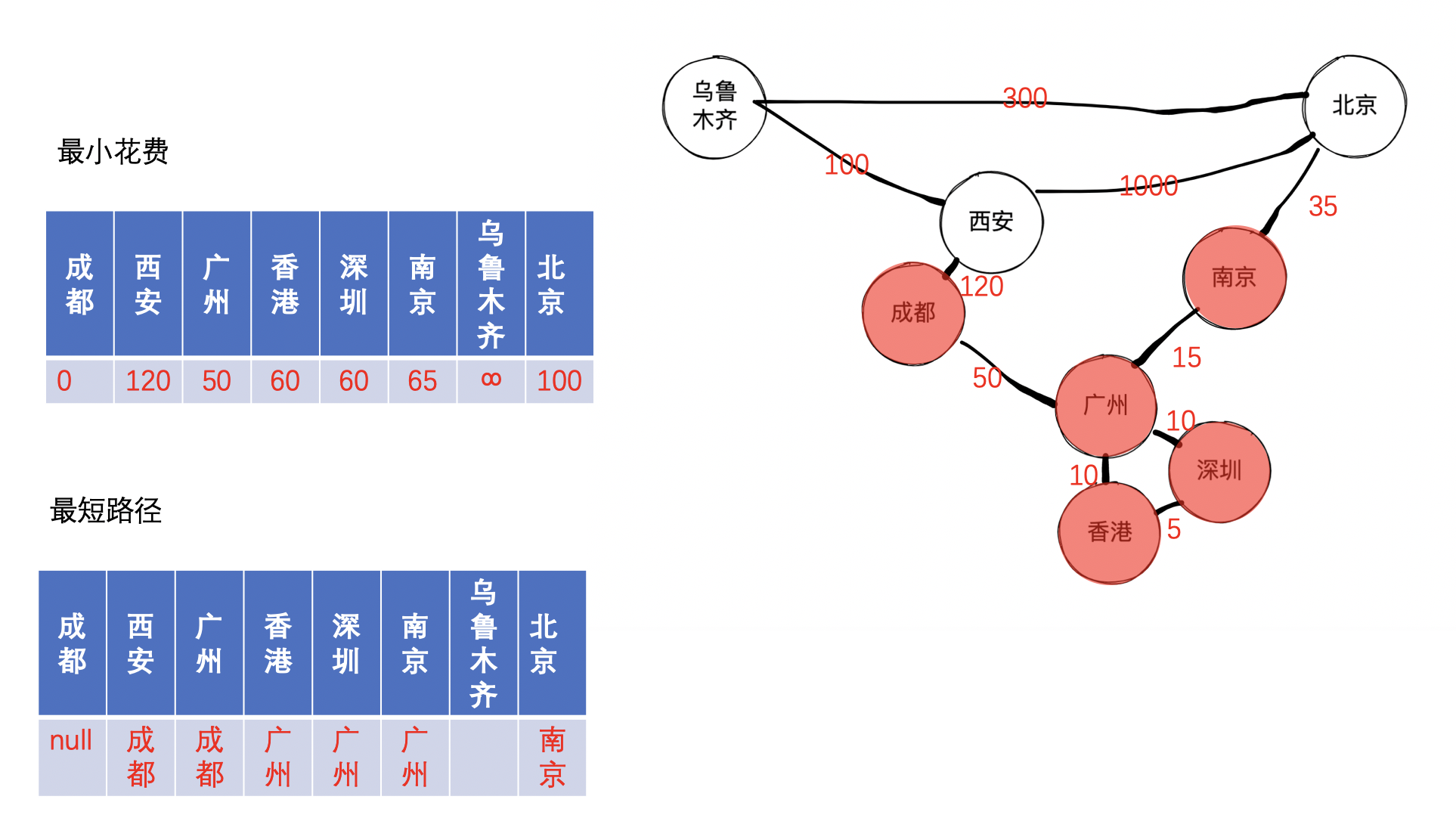
接着，我们找到未收录节点中的最小的节点，经过查找，找到的是北京，因为发现成都到乌鲁木齐的距离由原来的无穷大变成经过北京再到乌鲁木齐，因此可以更新距离和路径，可以得到如下图：

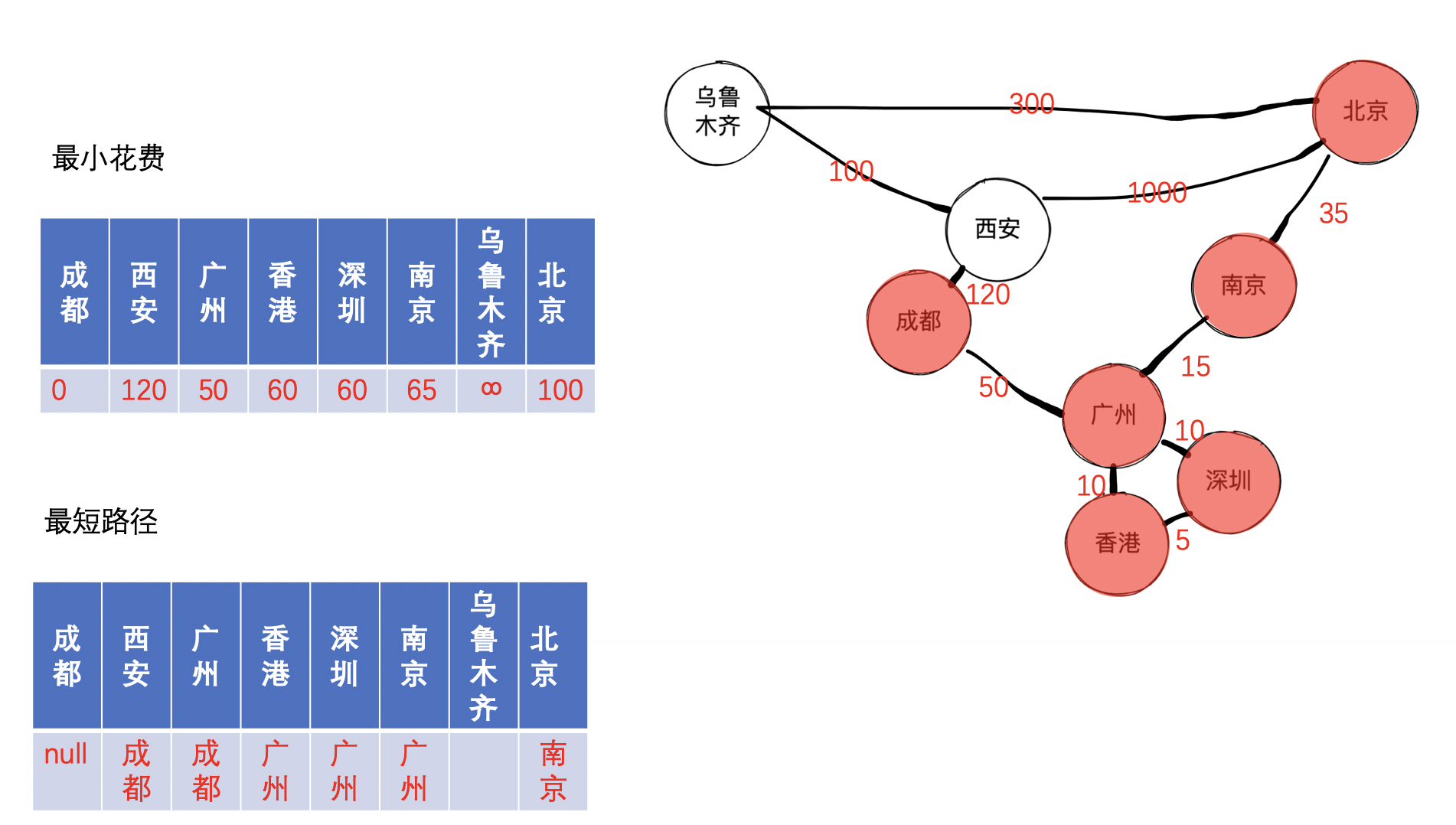
接着，我们找到未收录节点中的最小的节点，经过查找，找到的是乌鲁木齐，因为发现成都到西安的距离可以保持不变，因此可以不更新距离和路径，可以得到如下图：

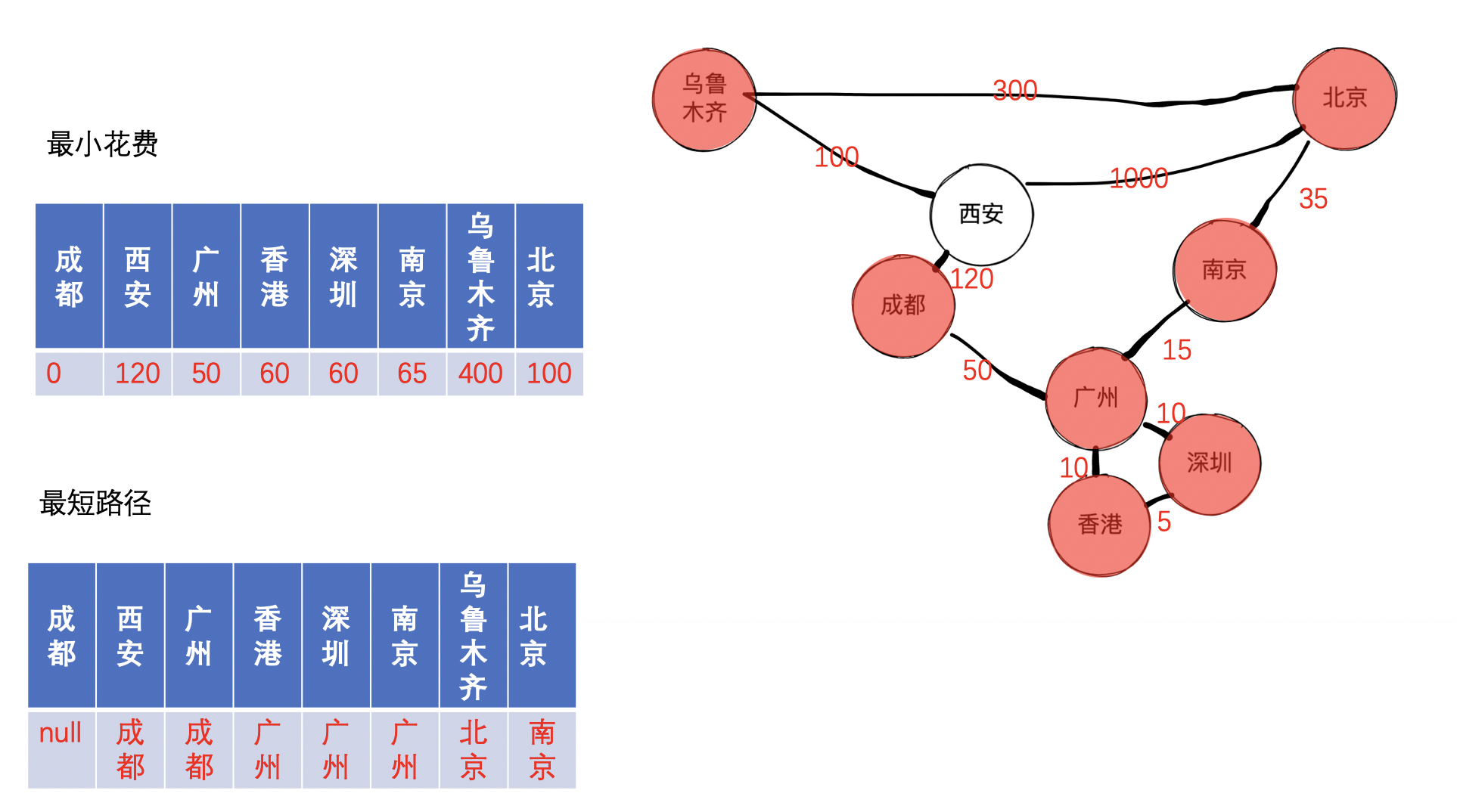
接着，我们找到未收录节点中的最小的节点，经过查找，找到的是西安，因为发现成都到乌鲁木齐的距离可以变得更小，因此可以更新成都到乌鲁木齐距离，并且把西安更新到成都到乌鲁木齐的路径上，可以得到如下图：

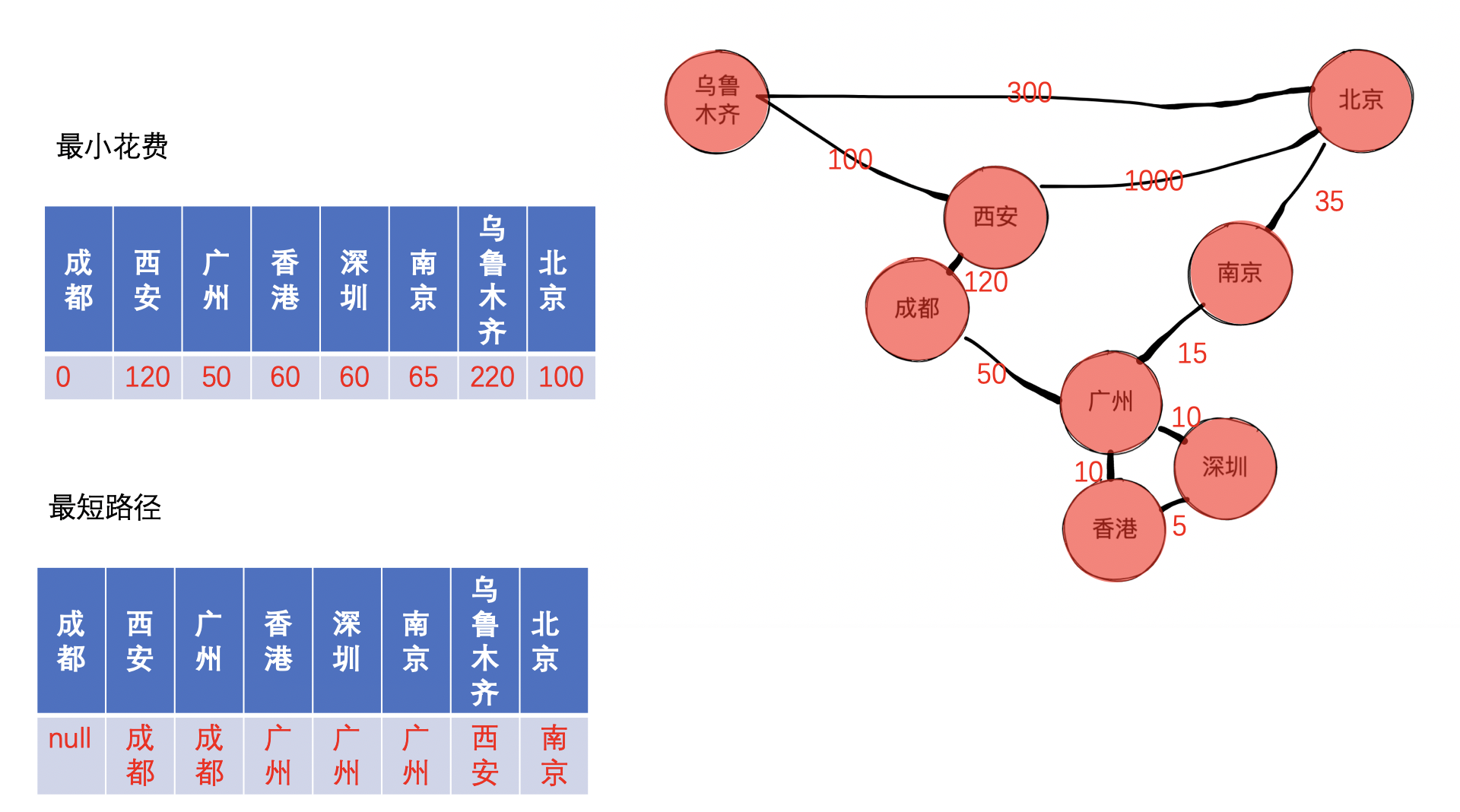
到现在，我们已经把所有的顶点都收录完成了，因此，找不到未收录的最小顶点，退出循环，程序结束。

分析了上面的流程，我们就可以写出迪杰斯特拉算法的伪代码了，如下：

/* 单源有权最短路径算法 */
function dijkstra(vertex) {
  collected[vertex] = true;
  for(图中所有顶点 V) {
    if(当前 V 是 vertex的邻接点) {
      distance[V] = vertex到V的权重
      把 V 更新在 vertex的路径上
    } else {
      distance[V] = 无穷大
    }
  }
  while(true) {
    minVertex = 找出未收录顶点的最小者；
    if(找不到这样的minVertex) {
      break;
    }
    collected[minVertex] = true;
    for(minVertex 的每个邻接点 neighborVertex) {
      if(!collected[neighborVertex]) {
        if(存在负值圈) {
          return false;
        }
        if(distance[minVertex] + minVertex到neighborVertex的权重 < distance[neighborVertex]) {
          distance[neighborVertex] = distance[neighborVertex] + minVertex到neighborVertex的权重
          path[neighborVertex] = minVertex
        }
      }
    }
  }
  return true;
}

可以看到的是，迪杰斯特拉算法还是基于广度优先的思想在做的，不过神奇的是却没有用到队列，是基于贪心算法的思想，对此有兴趣的同学可以自行查阅相关资料。

需要注意的是，迪杰斯特拉算法是不能解决负值圈的问题的，就好比，你每在那个地方兜一下，不仅不花钱，别人还要倒给你钱，只要你不断兜圈子，那这儿的权重就会变成负无穷。

还有一个需要大家注意的问题是，对于辅助函数findMinDist，每次都找最小值，这个操作我们是否已经在哪儿见过了呀？很容易就联想到，可以引入最小堆来加快每次查找最小未收录节点的效率。

和无权图的情况类似，不管是有向图还是无向图，都可以使用迪杰斯特拉算法进行求解。

带权图多源最短路径算法

迪杰斯特拉算法解决的是单源最短路径的问题，如何求多源最短路径呢，有的朋友会说，那直接把迪杰斯特拉算法对每个顶点都进行一次求解就可以了啊，这个确实是可以的，但是，还可以有更高明的算法，这就是接下来要阐述的弗洛伊德算法。

不幸的消息又来了，弗洛伊德算法是基于动态规划思想的，在前文我们阐述KMP的时候提到过next数组的求解过程也是基于动态规划的，这是一个老大难问题，这方面比较小白的朋友，可以先尝试学习这门课程 (opens new window)，然后再回过来看这篇博客较好。

既然是基于动态规划，那么就一定是存在递推关系的，接下来就看一看这个递推关系是怎么建立的。

令：Dp^k[i][j] = 路径 {i->{l<=k}->j}的最小长度，和迪杰斯特拉算法一样，这儿只是表示已经收进到集合中的当前编号小于等于k的顶点从i到j的最短路径。

那么，Dp⁰[i][j]，Dp¹[i][j]，... Dp^size-1[i][j]给出了i到j真正的最短距离，size为图中的顶点个数。

当 Dp^k-1[i][j]已经完成，递推到 Dp^k[i][j]时，存在下面两种情况：

如果 k∉ 最短路径{i->{l<=k}->j}，则 Dp^k-1[i][j] = Dp^k[i][j]

如果 k∈ 最短路径{i->{l<=k}->j}，则该路径必定由两段最短路径组成，即： Dp^k[i][j] = Dp^k-1[i][k] + Dp^k-1[k][i](最外层循环控制序列，内两层循环控制两点，所以在求 Dp^k[i][j]时，一定已经求出了 Dp^k-1[i][k] 和 Dp^k-1[k][i])

如果使用邻接矩阵表示图的话，弗洛伊德算法代码看起来会比较简洁，但是我们依然使用上面的那种表示方法，那么实现就如下：

/**
 * 弗洛伊德算法
 * @param {Graph} graph
 */
function floyd(graph) {
  // 根据图中最大的顶点数初始化dp数组
  let size = graph.vertexList.length;
  // 初始化无穷大，为了在日后的计算中将最短距离缩小，dp[i][j]的意义就是任意两点i和j之间的最短距离
  const dp = Array.from({
    length: size,
  }).map(() => {
    return Array.from({
      length: size,
    }).fill(Infinity);
  });
  // 初始化为-1，代表两点之间不存在中间节点
  const path = Array.from({
    length: size,
  }).map(() => {
    return Array.from({
      length: size,
    }).fill(-1);
  });
  /**
   * 定义一个求两点之间最短路径的函数
   * @param {Vertex} start
   * @param {Vertex} end
   * @returns
   */
  const getShortestPath = (start, end) => {
    const shortestPath = (i, j) => {
      let k = path[i][j];
      // 如果两点之间不存在中间节点
      if (k < 0) {
        return (
          graph.vertexList[i].cityName + "->" + graph.vertexList[j].cityName
        );
      }
      // 从i到k的路径
      const leftVia = shortestPath(i, k);
      // 从k到j的路径
      const rightVia = shortestPath(k, j);
      // 因为计算途径路径的时候，多算了一个k节点，因此，需要给它替换掉
      const via = leftVia + "->" + rightVia.replace(/^[\u4e00-\u9fa5]+->/, "");
      return via;
    };
    const i = graph.vertexList.findIndex((v) => v === start);
    const j = graph.vertexList.findIndex((v) => v === end);
    if (i < 0 || j < 0) {
      return "";
    }
    return shortestPath(i, j);
  };
  /**
   * 定义一个求两点之间最小化肥的函数
   * @param {Vertex} start
   * @param {Vertex} end
   */
  const getShortestDistance = (start, end) => {
    const i = graph.vertexList.findIndex((v) => v === start);
    const j = graph.vertexList.findIndex((v) => v === end);
    return i >= 0 && j >= 0 ? dp[i][j] : null;
  };
  // 初始化dp的值，若两点之间存在边，则初始化为权重，若不存在边，则初始为无穷大
  for (let i = 0; i < size; i++) {
    // 将对角线初始化为0，因为不允许自回路
    dp[i][i] = 0;
    const v1 = graph.vertexList[i];
    // 将存在邻接点的点初始化为两点之间的权重，若不存在则初始化为无穷大
    v1.edges.forEach((edge) => {
      const j = graph.vertexList.findIndex((x) => x === edge.to);
      dp[i][j] = edge.cost;
    });
  }
  /**
   * 错误断言函数
   */
  const assertError = () => {
    throw new Error("存在负值圈，无法计算");
  };
  for (k = 0; k < size; k++) {
    for (i = 0; i < size; i++) {
      for (j = 0; j < size; j++) {
        // 将下标为k的节点加入{i->{l<=k}->j}的集合中，如果从i到k的距离和k到j的距离比当前的小，则更新i到j的最短距离，并且i和j之间的最短距离是从i到k再到k到j
        if (dp[i][k] + dp[k][j] < dp[i][j]) {
          dp[i][j] = dp[i][k] + dp[k][j];
          if (i == j && dp[i][j] < 0) {
            /* 若发现负值圈，不能正确解决，返回错误标记 */
            return {
              distance: assertError,
              path: assertError,
            };
          }
          // 将k更新在i和j之间，表示从i到j必须要途径k节点
          path[i][j] = k;
        }
      }
    }
  }
  return {
    distance: getShortestDistance,
    path: getShortestPath,
  };
}

可以看到，我们一直都在不断地去找顶点的序号，因此，使用邻接矩阵表示的话，这个过程是可以省略的，所以代码会更简洁一些。

上述是对于动态规划的理论描述，如果有同学看起来觉得困难的话，不如先看下文，然后再回过头来看理论描述。

弗洛伊德算法首先先求出任意两点A和B间的距离，然后两点之间加入一个新的点C，原来A和B的距离是否能够被A+C和B+C替换（这就好比把一段线段逐渐打成由几个线段组成的一个过程）。

最外层的循环k其实控制的是对于开始节点i和结束节点j，加入新的节点的个数，随着节点不断地被加入，便可以不断的优化i到j之间的最短距离，最终解出两点之间的最短距离。

比如我们求成都到北京的距离，首先，我们已知北京到西安，西安到成都，南京到北京，南京到广州，广州到成都等城市之间的距离。

首先将北京和成都不存在邻接关系，因此两者之间的距离初始化为正无穷，假设现在我们加入深圳，对北京到成都的距离没有影响（别的城市距离有影响，但我们现在只阐述北京到成都，后续将不再赘述），接着加入南京，可以将北京到广州的距离更新为 50，紧接着，我们加入乌鲁木齐，对于北京到成都的距离没有影响，接着我们加入西安，此时北京到成都的距离可以更新为 1120，假设现在我们加入广州，成都到北京的距离可以更新为 100，后面，我们再加入香港，对于北京到成都的距离已经没有影响了，因此，北京到成都的距离就求解完毕了。

由于这是一个动态的过程，每时每刻都在求以k个顶点为集合中的任意两点间距离，当所有的顶点都加入完毕的时候，就可以求得所有的任意两点间的距离。